AL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
1 tháng 12 2018
Chọn C.
Gọi q là công bội của cấp số. Khi đó ta có:
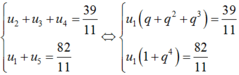
Suy ra: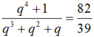 
⇔ 39q4 – 82q3 -82q2 -82q + 39 = 0
⇔ (3q – 1)(q – 3)(13q2 + 16q + 13) = 0 ⇔ q = 1/3, q = 3
PT
1
CM
25 tháng 8 2018
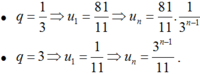
Ta có
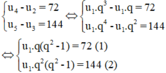
Lấy (2) chia (1) theo vế với vế ta được q = 2 thế vào (1):
(1) ⇔ 2u1(4 – 1) = 72 ⇔ u1 = 12
Vậy u1 = 12 và q = 2
CM
27 tháng 8 2017
Chọn B.
Với q = 3 ta có: 
nên có một số hạng của dãy
Với q = 1/3 ta có: 
nên có một số hạng của dãy.
CM
11 tháng 5 2018
Chọn C
Gọi q là công bội của cấp số. Khi đó ta có
u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11
⇔ u 2 + u 3 + u 4 = 39 11 u 1 + u 5 = 82 11 ⇔ u 1 q + q 2 + q 3 = 39 11 u 1 1 + q 4 = 82 11
Suy ra:
q 4 + 1 q 3 + q 2 + q = 82 39 ⇔ 39 q 4 − 82 q 3 − 82 q 2 − 82 q + 39 = 0
⇔ ( 3 q − 1 ) ( q − 3 ) ( 13 q 2 + 16 q + 13 ) = 0 ⇔ q = 1 3 , q = 3
q = 1 3 ⇒ u 1 = 81 11 ⇒ u n = 81 11 . 1 3 n − 1
q = 3 ⇒ u 1 = 1 11 ⇒ u n = 3 n − 1 11
PT
1
CM
9 tháng 10 2017
Chọn C.
Công thức tổng quát của CSN có số hạng đầu là u1 và công bội q
u n = u 1 . q n - 1
Cách giải:
Gọi số hạng đầu và công bội của CSN lần lượt là u 1 , q
Theo đề bài ta có hệ phương trình:
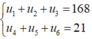
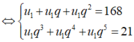
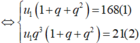
Lây (2) chia cho (1) ta được:
CM
5 tháng 12 2019
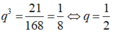
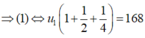
Ta có:
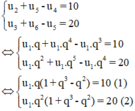
Lấy (2) chia (1) theo vế với vế ta được q = 2 thế vào (1):
(1) ⇔ 2u1(1 + 8 - 4) = 10 ⇔ u1 = 1
Vậy u1 = 1 và q = 2
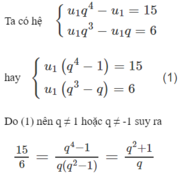
Theo t/c CSN \(u_1u_3=u_2^2\Rightarrow u_2^3=64\Rightarrow u_2=4\)
\(\Rightarrow\left\{{}\begin{matrix}u_1+u_3=10\\u_1u_3=16\end{matrix}\right.\)
Theo Viet đảo, \(u_1\) và \(u_3\) là nghiệm: \(t^2-10t+16=0\Rightarrow\left[{}\begin{matrix}t=2\\t=8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}u_1=2\Rightarrow q=2\\u_1=8\Rightarrow q=\frac{1}{2}\end{matrix}\right.\)