abc x(x+12)=abcabc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt Albert; Bernard; Cheryl laf A;B;C
Trong số 10 đáp án có ngày 18 và 19 chỉ xuất hiện 1 lần nếu sinh nhật của C vào hai ngày này chắc chắn B đã biết=>Loại 19/5 và 18/6
Nếu C nói với A tháng sinh là tháng 5 hoặc tháng 6 thì sinh nhật của C chỉ có thể là 19/5 hoặc 18/6
và B biết đáp án nhưng A khẳng định B không biết=> C noí với A tháng sinh của cô ấy là 7 hoặc 8
=>Loại tiếp 15/5;16/5;17/6
+) Trong số những ngày còn lại từ 15 đến 17 tháng 7 hoặc 8 ngày 14 xuất hiện 2 lần
Nếu C nói với B sinh nhật cô ấy là ngày 14 thì B không thể biết đáp án nhưng B lại biết=>Loại tiếp 14/7 và 14/8
Vậy còn 16/7;15/8;17/8
Sau câu nói của B thì A cũng biết=>Ngày đó 16/7 vì nếu C nói sinh nhật cô ấy vào tháng 8 thì A không thể biết vì có tới 2 ngày trong tháng 8
Vậy sinh nhật của C là 16/7

a)
`(2x-3)(x+4)>2(x^2 +1)`
`<=>2x^2 +8x-3x-12>2x^2 +2`
`<=>5x>14`
`<=>x>14/5`
//////////////////////l/////////////l---------->
`0` `14/5`
b)
`(3x-1)/2-(5x+1)/3>4`
`<=>(9x-3)/6-(10x+2)/6>24/6`
`<=>9x-3-10x-2>24`
`<=>-x>29`
`<=>x<-29`
-------------l////////////////l////////////////////
-29 0

Để : \((n+5)⋮(n-2)\left(+\right)\)
\(\Leftrightarrow\dfrac{n+5}{n-2}\inℤ\Leftrightarrow\dfrac{n-2+7}{n-2}\inℤ\)
\(\Leftrightarrow1+\dfrac{7}{n-2}\inℤ\)
Vì \(1\inℤ\) nên để \(\left(+\right)\inℤ\)
\(\Leftrightarrow\dfrac{7}{n-2}\inℤ\)
\(\Leftrightarrow7⋮\left(n-2\right)\)
\(\Leftrightarrow\left(n-2\right)\inƯ\left(7\right)\)
Ta có : \(Ư\left(7\right)=\left(\pm1;\pm7\right)\)
Lập bảng ra ta thấy : Các giá trị n thoả mãn là :
\(n\in\left\{3;1;10;-5\right\}\)
\(Vậy.........\)
Theo đề (n+5)⋮(n−2)
(n+5) –(n-2)⋮(n−2)
n+5 –n-2⋮(n−2)
7 ⋮ n-2
Nên (n-2) ϵ {-1; 1; -7; 7}
Vậy n ϵ {1; 3; -5; 9}

Lượng nước mà vòi đó cần chảy thêm để đầy bể là:
1 - 3/4 = 1/4 (thể tích bể)
Để chảy đầy bể từ 9h18p vòi đó mất:
(1/4 : 1/3) x 1= 3/4 (giờ) = 45 phút
Vòi đó chảy đầy bể vào lúc:
9 giờ 18 phút + 45 phút = 9 giờ 63 phút = 10 giờ 3 phút
Đ.số: 10 giờ 3 phút

Để tìm phân số có mẫu là 10, lớn hơn -3/4 và bé hơn -3/5, ta cần tìm một phân số âm có tử số nhỏ hơn mẫu số và lớn hơn -3/4.
Ta có thể chọn phân số -2/10. Vì -2/10 = -1/5 và -1/5 lớn hơn -3/4 và bé hơn -3/5.
Vậy, phân số cần tìm là -2/10.

Số phần tử của không gian mẫu \(\left|\Omega\right|=C^3_{19}\)
Gọi A là biến cố: "An chọn ra 3 quả cho tổng chia hết cho 4."
Trong các số từ 1 đến 19 sẽ có 4 số chia hết cho 4; 5 số chia 4 dư 1; 5 số chia 4 dư 2 và 5 số chia 4 dư 3. Để tổng các số trên 3 quả chia hết cho 4 thì số dư của bộ số đó khi chia cho 4 (ta gọi là \(\left(a,b,c\right)\)) phải bằng 1 trong các bộ số sau:
\(\left(0,0,0\right)\), \(\left(0,1,3\right),\left(0,2,2\right),\left(1,1,2\right),\left(3,3,2\right)\).
Với TH \(\left(a,b,c\right)\rightarrow\left(0,0,0\right)\) thì có tất cả \(C^3_4=4\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(0,1,3\right)\) thì có tất cả \(4.5^2=100\) cách chọn
Với TH \(\left(a,b,c\right)\rightarrow\left(0,2,2\right)\) thì có tất cả \(4.C^2_5=40\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(1,1,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(3,3,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Vậy \(\left|A\right|=4+100+40+50+50=244\).
\(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{244}{C^3_{19}}=\dfrac{244}{969}\).
Vậy xác suất để An chọn ra 3 quả có tổng chia hết cho 4 là \(\dfrac{244}{969}\)

a, để tính tổng A = 1 + 2 + 3 + 4 + … + 99 + 100, ta áp dụng công thức tổng của dãy số từ 1 đến n: S = (n * (n + 1)) / 2.
Với n = 100, ta có: A = (100 * (100 + 1)) / 2 = 5050.
b, để tính tổng B = 4 + 7 + 10 + 13 + … + 301, ta nhận thấy các số trong dãy này tạo thành một cấp số cộng với công sai d = 3.
Ta có công thức tổng của cấp số cộng: S = (n/2) * (a + l), trong đó n là số phần tử, a là số đầu tiên, l là số cuối cùng.
Số đầu tiên a = 4, số cuối cùng l = 301, và công sai d = 3.
Số phần tử n = ((l - a) / d) + 1 = ((301 - 4) / 3) + 1 = 100.
Vậy tổng B = (100/2) * (4 + 301) = 50 * 305 = 15250.
B2, để tính tổng của tất cả các số tự nhiên x, biết x là số có 2 chữ số và 12 < x < 91, ta cần tính tổng các số từ 13 đến 90.
Áp dụng công thức tổng của dãy số từ a đến b: S = ((b - a + 1) * (a + b)) / 2.
Với a = 13 và b = 90, ta có: S = ((90 - 13 + 1) * (13 + 90)) / 2 = (78 * 103) / 2 = 4014.
B3, để tính tổng của tất cả các số tự nhiên a, biết a có 3 chữ số và 119 < a < 501, ta cần tính tổng các số từ 120 đến 500.
Áp dụng công thức tổng của dãy số từ a đến b: S = ((b - a + 1) * (a + b)) / 2.
Với a = 120 và b = 500, ta có: S = ((500 - 120 + 1) * (120 + 500)) / 2 = (381 * 620) / 2 = 118260.

Số tiền còn lại sau khi ủng hộ quỹ: 1,570,000 - 500,000 = 1,070,000 đồng
Số tiền mẹ bù thêm: 712,000 đồng
Số tiền Tùng Lâm đã mua đôi giày: 1,070,000 + 712,000 = 1,782,000 đồng
Vậy đôi giày của Tùng Lâm đã mua với số tiền là 1,782,000 đồng.
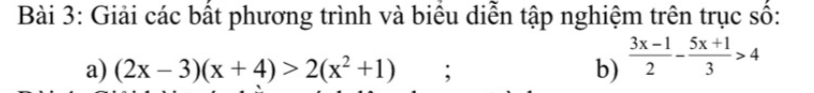
Đề chưa rõ ràng. Bạn coi lại.