Sắp xếp các giá trị theo thứ tự không giảm:

$0,290$   $0,398$   $0,399$   $0,401$   $0,402$   $0,402$   $0,405$   $0,406$   $0,408$   $0,410$

Tứ phân vị thứ nhất là $399$, tứ phân vị thứ ba là $406$, do đó ${\Delta }^Q=7$.

Đoạn số liệu không bất thường là [$Q^1-1,5{\Delta }^Q$ ; $Q^3+1,5{\Delta }^Q$] = [$388,5$ ; $416,5$].

Theo đoạn số liệu không bất thường, ta thấy $0,209$ không thuộc đoạn này, do đó kết luận của Bình là hợp lí.

a) Vận động viên $A$ : Khoảng biến thiên $=2$, Độ lệch chuẩn $=0,7$.
Vận động viên $B$ : Khoảng biến thiên $=5$, Độ lệch chuẩn $\approx 1,64$.
b) Vì khoảng biến thiên, độ lệch chuẩn về thành tích của vận động viên $A$ đều nhỏ hơn của vận động viên $B$ nên dựa trên các tiêu chí này ta có thể kết luận vận động viên $A$ có thành tích ổn định hơn.

Điểm thi thấp nhất là $0$ , cao nhất là $10$ . Do đó, khoảng biến thiên là $10-0=10$.
Hầu hết các bạn trong lớp có điểm $5,6,7$ vì vậy dùng khoảng biến thiên để đo độ phân tán của dãy số liệu này sẽ không hợp lí.

Giá trị nhỏ nhất là $16,4$ .
Giá trị lớn nhất là $28,9$.
Khoảng biến thiên là: $R=28,9-16,4=12,5$.
Dãy số liệu sắp xếp theo thứ tự không giảm:
Trung vị là $Q^2=(23,7+24,6):2=24,15$.

Nửa dữ liệu bên trái $Q^2$ là:
   $16,4$    $17,0$    $18,2$    $20,2$    $21,4$    $23,7$
Do đó, $Q^1=(18,2+20,2):2=19,2$.
Nửa dữ liệu bên phải $Q^2$ là:
   $24,6$    $27,2$    $27,3$    $28,2$    $28,8$    $28,9$ 
Do đó, $Q^3=(27,3+28,2):2=27,75$.
Khoảng tứ phân vị cho mẫu số liệu là: ${\Delta }^Q=Q^3-Q^1=27,75-19,2=8,55$.

Số trung bình của mẫu số liệu là: $\bar{x}=\genfrac{}{}{0ex}{}{16,4+17,0+\dots +18,2}{12}\approx 23,49$.
Độ lệch chuẩn:
$s^1=\sqrt{\genfrac{}{}{0ex}{}{(16,4-23,49{)}^2+\dots +(18,2-23,49{)}^2}{12}}\approx 4,52$.
Làm tương tự với dãy số liệu về nhiệt độ trung bình cho các tháng tại Thành phố Hồ Chí Minh ta có:
Khoảng biến thiên: $R=3,2$.
Khoảng tứ phân vị là: ${\Delta }^Q=27,7-26,55=1,15$.
Độ lệch chuẩn $s^2=0,91$.

b) Khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn của dãy số liệu về nhiệt độ trung bình các tháng tại Thành phố Hồ Chí Minh đều nhỏ hơn các số đặc trưng này tại Hà Nội nên ta khẳng định rằng nhiệt độ trung bình các tháng ở Thành phố Hồ Chí Minh it biến động hơn.

chịu

chịu

vẽ pt đường thẳng x - 2y = 4 (d)

thay tọa độ điểm O(0;0) vào vế trái của pt đường thẳng (d)

ta có 0 < 4

vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

Vẽ đường thẳng $d$: $x - 2y - 4 = 0$.

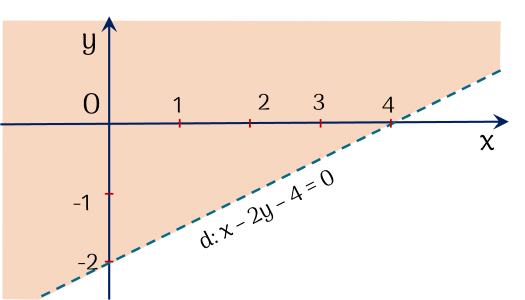
Ta thấy $(0 ; 0)$ là một nghiệm của BPT đã cho nên miền nghiệm của BPT là nửa mặt phẳng bờ $d$, chứa điểm $O(0 ; 0)$ và không kể bờ $d$ (phần tô màu trong hình vẽ trên).