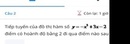
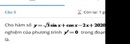
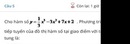
Giải phương trình
xy ' 1
biết
2
y x 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi tọa độ điểm , lần lượt là .
Hệ số góc tiếp tuyến của tại và lần lượt là
;
Để tiếp tuyến của tại và luôn song song với nhau điều kiện là
.
Ta có:
Do nên .
Trung điểm của đoạn là . Vậy đường thẳng luôn đi qua điểm cố định .
Ta có \(y'=-3x^2+6x-1\Rightarrow y^n=-6x+6;y^n=0\Leftrightarrow x=1\Rightarrow I\left(1;5\right)\) là điểm uốn của đồ thị (C)
G/s M (xM;yM); N(xN;yN) là 2 điểm di động trên (C)
Tiếp tuyển của (C) tại M,N song song với nhau
=> y'(xM)=y'(xN)
\(\Leftrightarrow-3x^2_M+6x_M-1=-3x_N^2+6x_N-1\)
\(\Leftrightarrow-3\left(x_M-x_N\right)\left(x_N+x_M\right)+6\left(x_M-x_N\right)=0\)
\(\Leftrightarrow\frac{x_M+x_N}{2}=1\left(x_M\ne x_N\right)\)=> I là trung điểm MN
Vậy đường thẳng MN luôn đi qua điểm I cố định

.
Đường thẳng là tiếp tuyến của đường cong khi hệ phương trình sau có nghiệm:
Mà tiếp tuyến của cắt trục hoành tại , cắt trục tung tại sao cho là tam giác vuông cân tại nên và
Từ và suy ra

Cho hàm số y=f(x)y=f(x)có đạo hàm liên tục trên khoảng K và có đồ thị là đường cong (C), phương trình tiếp tuyến của (C) tại điểm M(a,f(a)),(a∈K)M(a,f(a)),(a∈K) là:
y=f′(a)(x−a)+f(a).
.

Gọi là tiếp điểm của tiếp tuyến đã cho.
Phương trình tiếp tuyến có dạng: .
nên
và .
Phương trình tiếp tuyến là

Xét tiếp tuyênd với (C) tại điểm có hoành độ x0 bất kì trên (C)
Khi đó hệ số góc của tiếp tuyến đó là: y'=-x20-4x0-3=1-(x0+2) =< 1 với mọi x

TXĐ : R
y' =3x2 - 3
tiếp tuyến d song song với ox nếu hệ số góc bằng 0 nên ta có phương trình 0 = 3x2 -3 => x = 1 hoặc x= -1


xét m=1 và m=-1 thì pt luôn có nghiệm
xét m#1 và m#-1
đặt f(x)=(1−m2)x5−3x−1(1−m2)x5−3x−1
f(x)liên tục trên R nên f(x) lt trên [-1,0]
f(-1)=m2+1m2+1>0
f(0)=-1
f(-1)*f(0)<0 suyra ( đpcm ) .