Cho dãy số thực dương (xn). Chứng minh rằng tồn tại vô số số nguyên dương n thỏa mãn \(1+x_n>\sqrt[n]{2}x_{n-1}\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 6 2023
Tranh do học sinh được đồ họa bằng máy tính thì có được tham gia không cô?
CT
Cô Tuyết Ngọc
Manager
VIP
27 tháng 6 2023
Khuyến khích các em sáng tạo không giới hạn, nên các em có thể vẽ tranh bằng đồ họa máy tính nhé.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
27 tháng 6 2023
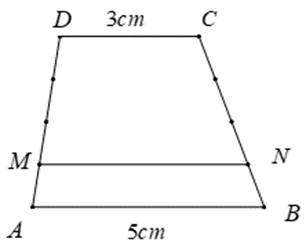
Hai tg ACD và tg ABC có đường cao từ A->CD = đường cao từ C->AB nên
\(\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{CD}{AB}=\dfrac{3}{5}\)
\(S_{ABCD}=S_{ACD}+S_{BCD}\)
\(\Rightarrow S_{ACD}=\dfrac{3}{3+5}xS_{ABCD}=\dfrac{3}{8}xS_{ABCD}=\dfrac{3}{8}x16=6cm^2\)
\(\Rightarrow S_{ABC}=S_{ABCD}-S_{ACD}=16-6=10cm^2\)
Hai tg ACD và tg BCD có đường cao từ A->CD = đường cao từ B->CD và chung cạnh CD
\(\Rightarrow S_{ACD}=S_{BCD}=6cm^2\)
C/m tương tự ta cũng có
\(S_{ABC}=S_{ABD}=10cm^2\)
Hai tg ABN và tg ABC có chung đường cao từ A->BC nên
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{BN}{BC}=\dfrac{1}{4}\Rightarrow S_{ABN}=\dfrac{1}{4}xS_{ABC}=\dfrac{1}{4}x10=2,5cm^2\)
đường cao từ N->AB là
\(\dfrac{2xS_{ABN}}{AB}=\dfrac{2x2,5}{5}=1cm\)
Hai tg NCD và tg BCD có chung đường cao từ D->BC nên
\(\dfrac{S_{NCD}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{4}\Rightarrow S_{NCD}=\dfrac{3}{4}xS_{BCD}=\dfrac{3}{4}x6=4,5cm^2\)
\(S_{ADN}=S_{ABCD}-S_{ABN}-S_{CDN}=16-2,5-4,5=9cm^2\)
Hai tg AMN và tg ADN có chung đường cao từ N->AD nên
\(\dfrac{S_{AMN}}{S_{ADN}}=\dfrac{AM}{AD}=\dfrac{1}{4}\Rightarrow S_{AMN}=\dfrac{1}{4}xS_{ADN}=\dfrac{1}{4}x9=2.25cm^2\)
\(S_{ABNM}=S_{ABN}+S_{AMN}=2,5+2,25=4,75cm^2\)
Như vậy ta biết diện tích hình thang ABNM, biết đáy lớn AB, biết đường cao (đường cao từ N->AB). Áp dụng công thức tính diện tích hình thang sẽ tính được đáy nhỏ MN.
Bạn tự tính nốt nhé
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
23 tháng 6 2023
CẬP NHẬT: MỖI TÀI KHOẢN DỰ THI CHỈ NỘP 01 BÀI DỰ THI CHỈNH CHU, TOÀN DIỆN NHẤT CÁC EM NHÉ!
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
23 tháng 6 2023
Thời gian nhận bài dự thi khá là lâu (khoảng 24 ngày), các bạn rủ bạn bè tham gia nữa nhé! Giải thưởng trên có thể chỉ là dự kiến, nếu có nhiều bài dự thi chất lượng thì có thể tăng giải thưởng thêm hi!
22 tháng 6 2023
Chúc anh chị 2005 sắp tới sẽ có 1 tinh thần tốt, sức khoẻ tốt để chiển mọi đề thi.
Và đừng quên xem Kaito Kid và 21:00 ngày 27/06/23 nha.
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 6 2023
Đường link tham khảo: Có nên "khoanh lụi" thi THPTQG hay không?
https://www.youtube.com/watch?v=gETeWVaK-E8
TL
22 tháng 6 2023
\(n\left(\Omega\right)=4^{50}\)
Nếu bạn An bị điểm liệt thì số câu đúng mà bạn chọn được bé hơn hoặc bằng 5, hay số câu sai lớn hơn hoặc bằng 45.
Gọi biến cố A: "bạn An không bị điểm liệt"
\(n\left(\overline{A}\right)=C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}\)
Xác suất để bạn An không bị điểm liệt
\(P\left(A\right)=1-\dfrac{n\left(\overline{A}\right)}{n\left(\Omega\right)}\)
\(=1-\dfrac{C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}}{4^{50}}\)
\(\approx0,99295\)
QT
Quoc Tran Anh Le
Giáo viên
19 tháng 6 2023
Chúng mình sẽ làm giấy chứng nhận cho 6 bạn đạt giải cao nhất nhé! Chi tiết về thời gian trả giấy, chúng mình sẽ thông báo sau.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
19 tháng 6 2023
Chúc mừng các bạn đạt giải thưởng cao nhé, có những cái tên quen thuộc nhưng cũng có những cái tên mới. Hy vọng các bạn, các em sẽ đồng hành cùng cuộc thi cũng như website nhé!
cái này toán 10 hay s v :(
không phải là toán lớp 5 ạ