Số nghiệm của phương trình trên một khoảng SVIP

I. Định lý

Định lý

Hệ quả

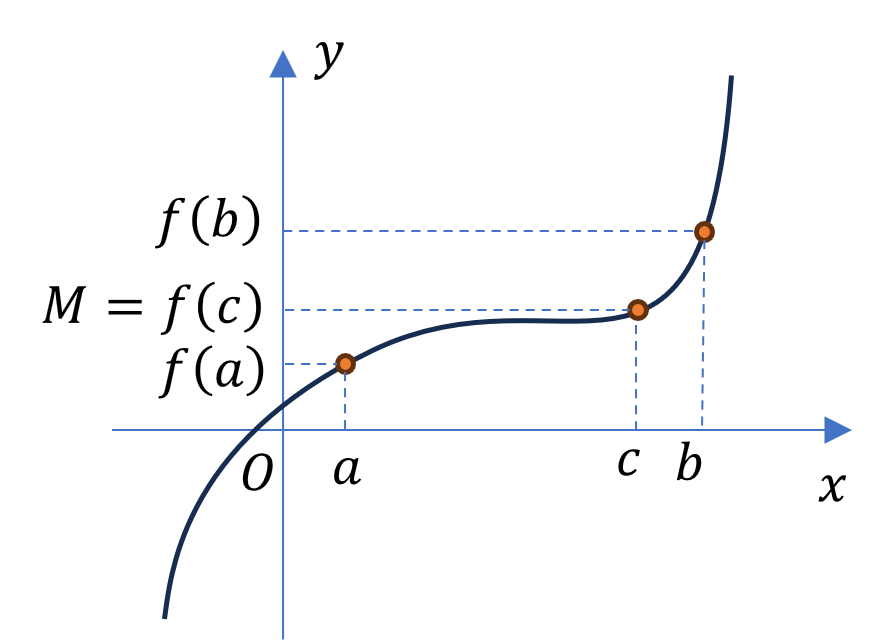
Nếu hàm số $y=f(x)$ liên tục trên đoạn $[a ; b]$ và $f(a) \cdot f(b)<0$ thì tồn tại ít nhất một điểm $c \in(a ; b)$ sao cho $f(c)=0$

Nói cách khác: Nếu hàm số $y=f(x)$ liên tục trên đoạn $[a ; b]$ và $f(a) . f(b)<0$ thì phương trình $f(x)=0$ có ít nhất một nghiệm nằm trong khoảng $(a ; b)$.

II. Phương pháp giải bài tập

🔹 Chứng minh phương trình $f(x)=0$ có ít nhất một nghiệm

- Tìm hai số a và $b$ sao cho $f(a) \cdot f(b)<0$

- Hàm số $f(x)$ liên tục trên đoạn $[a ; b]$

- Phương trình $f(x)=0$ có ít nhất một nghiệm $x_0 \in(a ; b)$

🔹 Chứng minh phương trình $f(x)=0$ có ít nhất $k$ nghiệm

- Tìm $k$ cặp số $a_{i}, b_{i}$ sao cho các khoảng $\left(a_{i} ; b_{i}\right)$ rời nhau và

$f\left(a_{i}\right) f\left(b_{i}\right)<0, i=1, \ldots, k$

- Phương trình $f(x)=0$ có ít nhất một nghiệm $x_{i} \in\left(a_{i} ; b_{i}\right)$.

🔹 Khi phương trình $f(x)=0$ có chứa tham số thì cần chọn $a, b$ sao cho :

- $f(a), f(b)$ không còn chứa tham số hoặc chứa tham số nhưng dấu không đổi.

- Hoặc $f(a), f(b)$ còn chứa tham số nhưng tích $f(a)$. $f(b)$ luôn âm.

III. Các ví dụ

Ví dụ 1. Chứng minh phương trình $x^2 \sin x+x \cos x+1=0$ có ít nhất một nghiệm. 

Giải

Ta có hàm số $f(x)=x^2 \sin x+x \cos x+1$ liên tục trên $\mathbb{R}$ và $f(0) \cdot f(\pi)=-\pi+1<0$

Suy ra phương trình $f(x)=0$ có ít nhất một nghiệm thuộc $(0 ; \pi)$

Ví dụ 2. Tìm tất cả giá trị $m$ để phương trình sau có nghiệm: $m(x-1)(x+2)+2 x+1=0$.

Giải

Đặt $f(x)=m(x-1)(x+2)+2 x+1$.

Tập xác định: $D=\mathbb{R}$ nên hàm số liên tục trên $\mathbb{R}$.

Ta có: $f(1)=3 ; f(-2)=-3 \Rightarrow f(1) \cdot f(-2)<0$.

Vậy phương trình đã cho có nghiệm với mọi $m$.