

Thầy Tùng Dương
Giới thiệu về bản thân



































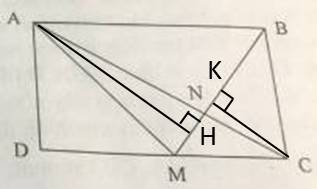
a) MC = 2/5 DC nên DC = 5/2 MC = 5/2 . 10 = 25 cm.
Do đó, AB = CD = 25 cm.
Hình thang ABCM có hai đáy AB, CM và chiều cao BC = AD = 21 cm.
Diện tích hình thang ABCM bằng: (25 + 10) x 21 : 2 = 367,5 (cm2)
b) Hạ AH \(\perp\) BM, CK \(\perp\) BM.
Ta có \(\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{AB}{MC}=\dfrac{5}{2}\) (vì cùng chiều cao, tỉ lệ diện tích bằng tỉ lệ hai đáy), do đó \(\dfrac{AH}{CK}=\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{5}{2}\) (chung đáy, tỉ lệ diện tích bằng tỉ lệ hai chiều cao)
\(\dfrac{S_{AMN}}{S_{CMN}}=\dfrac{AH}{CK}=\dfrac{5}{2}\Rightarrow\dfrac{S_{CMN}}{S_{AMC}}=\dfrac{2}{7}\)
\(S_{AMC}=\dfrac{1}{2}\times AD\times MC=\dfrac{1}{2}\times21\times10=105\left(cm^2\right)\)
\(S_{CMN}=\dfrac{2}{7}\times105=30\left(cm^2\right)\)
c) Hai tam giác ABH và ECH có:
HE = HA
\(\widehat{AHB}=\widehat{EHC}\) (đối đỉnh)
HB = HC
Suy ra: \(\Delta EBH=\Delta ECH\) (c.g.c).
Do đó \(\widehat{EBH}=\widehat{ECH}\) (hai góc tương ứng), mà hai góc này nằm ở vị trí so le trong nên AB // CE.
\(=\dfrac{1}{3}.\dfrac{3}{5}-\left(\dfrac{5}{6}\right)^2\\ =\dfrac{1}{5}-\dfrac{25}{36}\\ =-\dfrac{89}{180}\)
Dịch dấu phảy sang trái một hàng thì số A giảm đi 10 lần, tức là: B = A : 10 hay A = B x 10
Dịch dấu phảy sang phải một hàng thì số A tăng lên 10 lần, tức là: C = A x 10
Do đó, C = A x 10 = B x 10 x 10 = B x 100.
C - B = 100 x B - B = 99 x B
Vậy nên:
99 x B = 115,929
B = 115,929 : 99
B = 1,171
Vây A = 10 x 1,171 = 11,71.
Số tiền lãi là:
9000 x 20% = 1800 (đồng)
Vậy để lãi 20% so với giá mua, giá bán là:
9000 + 1800 = 10800 (đồng)
Gọi số trừ là \(\overline{A64}\), khi viết ngược trở thành \(\overline{A46}\).
\(\overline{A46}=A\times100+46\)
Theo bài ra ta có:
\(2108+\overline{A46}=2754\)
\(2108+A\times100+46=2754\)
\(A\times100=600\)
\(A=6\).
Số trừ ban đầu là: \(664\)
Phép tính ban đầu là: 2108 - 664 = 1444.
Do đặt bạn đó đặt các tích riêng thẳng cột với nhau nên thừa số nhân không phải là 345 mà đã bị trở thành 3 + 4 + 5 = 12.
Vậy, số thập phân là: 42,48 : 12 = 3,54.
Tích đúng là: 3,54 x 345 = 1221,3.
Tính được các góc \(\widehat{BAC}=80^{\circ};\widehat{MNP}=40^{\circ};\widehat{QSR}=80^{\circ};\widehat{IHK}=40^\circ\)
- Vì \(\widehat{B}=\widehat{P};\widehat{C}=\widehat{N};BC=NP\) nên \(\Delta ABC=\Delta MPN\quad\left(g.c.g\right)\)
Tương tự, \(\Delta ABC=\Delta FED\quad\left(g.c.g\right);\Delta MPN=\Delta FED\quad\left(g.c.g\right)\)
- Vì \(\widehat{Q}=\widehat{K};\widehat{S}=\widehat{I};QS=IK\) nên \(\Delta QSR=\Delta KHI\left(g.c.g\right)\)
Tổng ba số là: 45 x 3 = 135.
Tổng của số thứ hai và thứ ba là: 55 x 2 = 110.
Số thứ nhất là: 135 - 110 = 25.