xét △ABM và △ACM có

AB=AC (theo giả thiết)

\(\widehat{B}\) = \(\widehat{C}\) (theo giả thiết)

MB=MC (theo giả thiết)

⇒△ABM=△ACM (c.g.c)

⇒\(\widehat{AMB}\) = \(\widehat{AMC}\) (hai góc tương ứng)

\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\) chứng minh \(\left(\dfrac{a+b+c}{b+c+d}\right)^3=\dfrac{a}{d}\)

áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\Rightarrow\left(\dfrac{a+b+c}{b+c+d}\right)^3=\left(\dfrac{a}{b}\right)^3=\dfrac{a^3}{b^3}\left(1\right)\)

mà cần chứng minh: \(\left(\dfrac{a+b+c}{b+c+d}\right)=\dfrac{a}{d}\left(2\right)\)

từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\) \(\dfrac{a^3}{b^3}=\dfrac{a}{d}\Rightarrow a^3.d=b^3.a\)

                                        \(\Rightarrow a^2.d=b^3\)

vì \(\dfrac{a}{b}=\dfrac{b}{c}\Rightarrow a.c=b^2\)

                \(\Rightarrow a.b.c=b.c\left(3\right)\)

    \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow a.d=b.c\left(4\right)\)

từ \(\left(3\right)\) và \(\left(4\right)\) \(\Rightarrow a.a.d=b^3\)

                     \(\Rightarrow a^2.d=b^3\left(đpcm\right)\)

vậy \(\left(\dfrac{a+b+c}{b+c+d}\right)^3=\dfrac{a}{d}\)

\(\dfrac{0.375-0.3+\dfrac{3}{11}+\dfrac{3}{12}}{-0.625+0.5-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{1.5+1-0.75}{2.5+\dfrac{5}{3}-1.25}\)

=\(\dfrac{\dfrac{3}{8}-\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}}{-\dfrac{5}{8}+\dfrac{5}{10}-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{\dfrac{3}{2}+\dfrac{3}{3}-\dfrac{3}{4}}{\dfrac{5}{2}+\dfrac{5}{3}-\dfrac{5}{4}}\)

=\(\dfrac{3.\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}{-5.\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}+\dfrac{3\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}{5\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}\)

=\(\dfrac{3}{-5}+\dfrac{3}{5}\)

=\(0\)

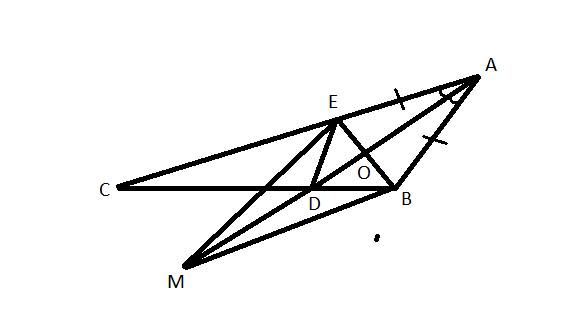
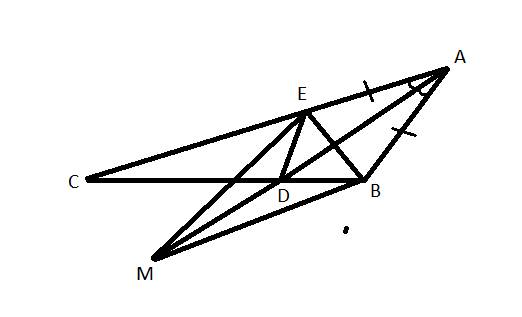
a,Xét △AED và △ABD có 

AE = AB (theo giả thiết)

EAD=BAD (theo giả thiết)

AD là cạnh chung 

⇒△AED = △ABD (c.g.c)

⇒DE = DB (hai cạnh tương ứng)

b, gọi o là giao điểm của AD và BE

Xét △AEO và △ABO có 

AE = AB (theo giả thiết)

EAO=BAO (theo giả thiết)

AO là cạnh chung 

⇒△AEO = △ABO (c.g.c)

⇒AOE = AOB (hai góc tương ứng)

ta có : AOE + AOB = 180 độ (hai góc kề bù)

          mà AOE = AOB

          ⇒AOE = AOB = 180 : 2 = 90

          ⇒ AO \(\perp\) EB hay AD \(\perp\) EB

c, vì AE = AB ⇒ △AEB cân tại A 

                      ⇒AEO = ABO

ta có : AEM = AEO + MEO

       ⇒MEO = AEM - AEO

          ABM = ABO + MB

       ⇒MBO = ABM - ABO

       mà AEO = ABO

       ⇒MEO = MBO

       ⇒△MEB cân tại M ⇒ME = MB

Xét △MEO và △MBO có 

ME = MB (chứng minh trên)

MOE = MOB = 90 độ

MO là cạnh chung 

⇒△MEO = △MBO (cạnh huyền - cạnh góc vuông)

⇒EMO = BMO (hai góc tương ứng)

Xét  △BDM và △EDM có 

ME = MB (chứng minh trên)

EMO = BMO (chứng minh trên)

MD là cạnh chung

⇒△BDM = △EDM (c.g.c)

mình trình bày rất mất thời gian nên nếu đúng thì tick mình nha

mình nhầm n=11 nhé 

\(3n-7⋮n+2\)

\(\Rightarrow3n+6-13⋮n+2\)

\(\Rightarrow3.\left(n+2\right)-13⋮n+2\)

Vì \(3.\left(n+2\right)⋮n+2\) \(\Rightarrow13⋮n+2\)

                               \(\Rightarrow n+2\inƯ\left(13\right)\)

                               \(\Rightarrow n+2\in\left\{1;13\right\}\)

Với \(n+2=1\)                         Với \(n+2=13\)

             \(n=1-2\)                                \(n=13-2\)

             \(n=-1\)                                   \(n=11\)

                          Vậy \(n=13\)