

Đào Thị Mộng Huyền
Giới thiệu về bản thân



































00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000=====================================================================================================================000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 hiểu chưa
1. (1−5+√2√2+1)⋅√3+2√2=−4√2+1√(√2+1)2=−4(1−5+22+1)⋅3+22=−42+1(2+1)2=−4.
2. Với x>0;x≠1x>0;x≠1 ta có:
A=(√xx+√x−1√x−1):2x+√x−2A=(xx+x−1x−1):2x+x−2
⇔A=(√x√x(√x+1)−1√x−1):2(√x−1)(√x+2)⇔A=(xx(x+1)−1x−1):2(x−1)(x+2)
⇔A=−2(√x−1)(√x+1)⋅(√x−1)(√x+2)2⇔A=−2(x−1)(x+1)⋅(x−1)(x+2)2
⇔A=−(√x+2)√x+1⇔A=−(x+2)x+1. Vạyy với x>0;x≠1x>0;x≠1, ta có A=−(√x+2)√x+1A=−(x+2)x+1.
ĐKXĐ: x≥1x≥1
Xét vế trái: (x−1)2≥0⇒√(x−1)2+1+√3(x−1)2+4≥√1+√4=3(x−1)2≥0⇒(x−1)2+1+3(x−1)2+4≥1+4=3
Xét vế phải √x−1≥0⇒3−√x−1≤3x−1≥0⇒3−x−1≤3
Vậy 2 vế cùng bằng 33 khi x=1x=1 (tmđk). Nghiệm của phương trình x=1
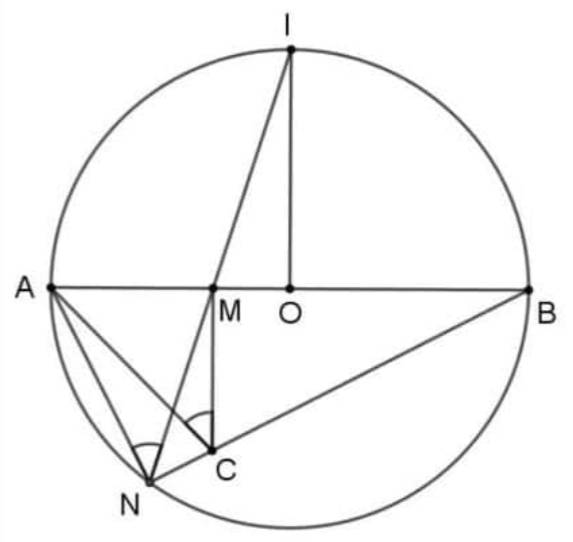
1) ˆAMC=90∘⇒A,M,CAMC^=90∘⇒A,M,C thuộc đường tròn đường kính ACAC
ˆANB=90∘⇒ˆANC=90∘⇒A,N,CANB^=90∘⇒ANC^=90∘⇒A,N,C thuộc đường tròn đường kính ACAC ⇒A,M,C,N⇒A,M,C,N cùng thuộc đường tròn đường kính ACAC.
2)Điểm II chính giữa cung AB⇒sAI=90∘AB⇒sAI⏜=90∘
ˆANIANI^ là góc nội tiếp chắn cung AI⇒ˆANI=12AI⇒ANI^=12 sđ AIAI⏜
⇒ˆANI=45∘⇒ˆANM=45∘⇒ANI^=45∘⇒ANM^=45∘
Chứng minh AM=MCAM=MC
Tứ giác AMCNAMCN nội tiếp ⇒ˆACM=ˆANM=45∘⇒ACM^=ANM^=45∘ (cùng chắn cung AMAM )
△AMC△AMC vuông tại M,ˆACM=45∘⇒△ACMM,ACM^=45∘⇒△ACM vuông cân tại MM
⇒AM=MC⇒AM=MC.
3) Chứng minh MN<RMN<R
MN=NI−IMMN=NI−IM. NI là dây không qua tâm ⇒NI<2R⇒NI<2R
IO⊥AB⇒IM>IO=RIO⊥AB⇒IM>IO=R (M khác OO, quan hệ đường xiên - đường vuông góc ) ⇒−IM<−R⇒MN=NI−IM<2R−R=R⇒−IM<−R⇒MN=NI−IM<2R−R=R.
1) Tìm tọa độ giao điểm của (d) và (P) khi m=2m=2
Thay m=2m=2 vào (d):y=2x+3(d):y=2x+3
Xét phương trình hoành độ giao điểm : x2−2x−3=0x2−2x−3=0
Giải phương trình tìm được x1=−1,x2=3x1=−1,x2=3
⇒⇒ Tọa độ giao điểm (−1;1)(−1;1) và (3;9)(3;9)
2) Xét phương trình hoành độ giao điểm: x2−mx−3=0x2−mx−3=0 (1).
Δ=m2+12.m2≥0⇒Δ=m2+12≥12>0. Δ=m2+12.m2≥0⇒Δ=m2+12≥12>0.
Vậy phương trình luôn có 2 nghiệm phân biệt ⇒(d)⇒(d) cắt (P)(P) tại 2 điểm phân biệt
x1,x2x1,x2 là 2 nghiệm của phương trình (1), theo hệ thức Vi - ét {x1+x2=mx1x2=−3{x1+x2=mx1x2=−3
y1=x21,y2=x22⇒x21+x22=4(x1+x2)+3⇔(x1+x2)2−2x1x2=4(x1+x2)+3y1=x12,y2=x22⇒x12+x22=4(x1+x2)+3⇔(x1+x2)2−2x1x2=4(x1+x2)+3
⇔m2+6=4m+3⇔m2−4m+3=0⇔[m=1m=3
Gọi vận tốc xe máy là x( km/x( km/ giờ )(x>0))(x>0)
Thời gian xe máy đi hết quãng đường: 120x120x (giờ)
Vận tốc ô tô: x+20x+20 (km/giờ)
⇒⇒ Thời gian ô tô đi hết quãng đường: 120x+20120x+20 (giờ)
Ô tô đến sớm hơn xe máy 1 giờ, ta có phương trình: 120x−120x+20=1120x−120x+20=1
Biến đổi đến phương trình: x2+20x−2400=0x2+20x−2400=0
Giải phương trình được: x1=40x1=40 (TM) và x2=−60x2=−60 (loại).
Vậy vận tốc xe máy là 40 km40 km /giờ, vận tốc ô tô là 60 km60 km /giờ
Bán kính đáy: 7:2=3,5 cm7:2=3,5 cm.
Thể tích sữa trong hộp: π×3,52×8≈3,14×3,52×8π×3,52×8≈3,14×3,52×8 =307,72 cm3=307,72ml=307,72 cm3=307,72ml.
1) Thay x=1x=1 vào biểu thức: A=√1+2√1−2A=1+21−2
A=−3A=−3
2) Chứng minh B=√x√x+2B=xx+2 với x≥0,x≠4x≥0,x≠4.
B=√x+2(√x−2)(√x+2)+(√x+1)(√x−2)(√x+2)(√x−2)−2√x(√x+2)(√x−2)B=x+2(x−2)(x+2)+(x+1)(x−2)(x+2)(x−2)−2x(x+2)(x−2)
=√x+2+x−√x−2−2√x(√x+2)(√x−2)=x−2√x(√x+2)(√x−2)=x+2+x−x−2−2x(x+2)(x−2)=x−2x(x+2)(x−2)
=√x(√x−2)(√x+2)(√x−2)=√x√x+2=x(x−2)(x+2)(x−2)=xx+2
3) Tìm xx để A⋅B≥0A⋅B≥0
A⋅B=√x+2√x−2⋅√x√x+2=√x√x−2A⋅B=x+2x−2⋅xx+2=xx−2.
TH1: x=0⇒√x=0⇒A⋅B=0x=0⇒x=0⇒A⋅B=0 (TM)
TH2: x>0⇒√x>0⇒√x−2>0⇒x>4x>0⇒x>0⇒x−2>0⇒x>4
Kết hợp điêu kiện: x=0x=0 hoặc x>4x>4 thỏa mãn yêu cầu.