Cho tam giác ABC, I là trung điểm của AB. Qua I kẻ đường thẳng song song với BC, nó cắt cạnh AC tại K. Qua K kẻ đường thẳng song song với AB, nó cắt cạnh BC tại H. CMR:
a/ tam giác AIK = tam giác KHC
b/ AK = KC và AK = IH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 12 2018
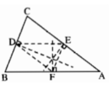
+)Xét tam giác BDF và ∆EFD có:
DF chung
∠BDF = ∠DFE ( hai góc so le trong; BC// EF)
∠BFD = ∠FDE ( hai góc so le trong; DE// AB)
Suy ra:∆ BDF = ∆EFD (g.c.g)
Suy ra BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.
+) Xét ∆ CDE và ∆ EFA có :
CD = EF ( chứng minh trên)
∠(CDE) = ∠(EFA) = ∠(CBA)
∠(ECD) = ∠(AEF) (các góc đồng vị).
Suy ra: ∆ CDE = ∆ EFA ( g.c.g)
Suy ra CE = EA nên E là trung điểm của CD.
18 tháng 5 2022
a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)
CM
8 tháng 2 2018
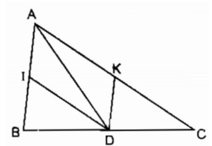
Ta có: DK // AB (gt)
hay DK // AI
DI // AC (gt)
hay DI // AK
Vậy tứ giác AIDK là hình bình hành
a/ Vì AK // IH nên AI = KH và AK = IH ( vì phần ghi nhớ ở bài 1 đó )
Vì IK // HC nên IK = HC và IH = KC
Xét tam giác AIK và tam giác IKH có:
\(\hept{\begin{cases}AI=KH\\IK:canh\\AK=IH\end{cases}}chung\)
suy ra tam giác AIK = tam giác HKI ( c.c.c )
Xét tam giác IKH và tam giác KHC có :
\(\hept{\begin{cases}IK=HC\\KH:canh\\IH=KC\end{cases}}chung\)
suy ra tam giác HKI = tam giác KHC ( c.c.c )
mà tam giác AIK = tam giác HKI
tam giác HKI = tam giác KHC
suy ra tam giác AIK = tam giac KHC( đpcm )
b/ Vì tam giác AIK = tam giác KHC
nên AK = CK ( vì là 2 cạnh tương ứng )
Vậy :........
hay AI = HK ( vì là 2 cạnh tương ứng )
mà AI = BI ( vì I là tring điểm của AB )
nên BI = HK ( = AI )
Vậy: ......
Vân Khánh đây là bài làm nhé! Nhớ k nghe! Thank you!!!
a) Nối IH
Xét 2 tam giác: \(\Delta\)BIH và \(\Delta\)KHI có
IH cạnh chung
\(\widehat{BIH}\)= \(\widehat{KHI}\)( so le trong do AB // KH)
\(\widehat{IHB}\)= \(\widehat{HIK}\)( so le trong do IK // BC)
suy ra \(\Delta\)BIH = \(\Delta\)KHI (g.c.g)
\(\Rightarrow\)IB = KH (2 cạnh tương ứng)
mà IB = IA nên IA = KH
\(\widehat{AIK}\)= \(\widehat{IBH}\)(đồng vị do IK // BC)
\(\widehat{IBH}\)= \(\widehat{KHC}\)(đồng vị do KH // AB)
suy ra \(\widehat{AIK}\)= \(\widehat{KHC}\)
Xét 2 tam giác: \(\Delta\)AIK và \(\Delta\)KHC có:
IA = HK (cmt)
\(\widehat{AIK}\)= \(\widehat{KHC}\)(cmt)
\(\widehat{IAK}\)= \(\widehat{HKC}\)(đồng vị do HK // AB)
suy ra \(\Delta\)AIK = \(\Delta\)KHC (g.c.g)
b) \(\Delta\)AIK = \(\Delta\)KHC (theo phần a) \(\Rightarrow\)AK = KC (2 cạnh tương ứng)
Xét \(\Delta\)AIK và \(\Delta\)HKI có:
AI = HK (cm)
\(\widehat{AIK}\)= \(\widehat{HKI}\)(so le trong do HK // AB)
IK cạnh chung
suy ra \(\Delta\)AIK = \(\Delta\)HKI (c.g.c)
\(\Rightarrow\)AK = IH (2 cạnh tương ứng)