chỉ từ các chữ số 1 , 2 , 3 , 4 , 5 lập được nhiều nhất bao nhiêu số tự nhiên lẽ khác nhau mà mỗi số đều có bốn chữ số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các số là:
2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320
2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563

Caau1 :
Trong hệ thập phân có 10 chữ số 0, 1, 2, ....9. Số tự nhiên không chia hết cho 5 là các số có hàng đơn vị khác 0 và 5.
Vì số tự nhiên đó có các chữ số khác nhau, nên:
+ Nếu số có 1 chữ số thì có 8 số (trừ 0 và 5)
+ Nếu số có 2 chữ số thì có 8 cách chọn hàng đơn vị (trừ 0 và 5), có 8 cách chọn chữ số hàng chục (trừ 0 và chữ số đã chọn hàng đv). Tổng cộng có 8 x 8 = 8 mũ 2 = 64 số
+ Nếu số có 3 chữ số thì có 8 cách chọn hàng đơn vị (trừ 0 và 5), có 8 cách chọn chữ số hàng trăm (trừ 0 và chữ số đã chọn hàng đv), có 8 cáh chọn chữ số hàng chục (trừ 2 chữ số đã chọn ở hàng trăm và hàng đv. Tổng cộng có 8 x 8 x 8 = 8 mũ 3 = 512 số
..............xin chữa lại:
+ Nếu số có 4 chữ số thì có 8 x 8 x 7 x 8 số
+ Nếu số có 5 chữ số thì có 8 x 8 x 7 x 6x 8 số
+ Nếu có 10 chữ số thì có 8 x 8 x 7x 6 x 5 x 4x3x2x1x8 số khác nhau không chia hết cho 5.
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~
Câu 2 :
số các số có chữ số hàng chục trùng với chữ số hàng đơn vị : 9 số ( tương ứng với 9 chữ số 1, 2,...., 9 )
nếu chữ số hàng chục là x thì số các số có hàng chục là x và có số hàng đơn vị nhỏ hơn cũng là x ( vì số các số tự nhiên liều trước của 1 số, kể cả số 0 bằng chính số đó )
vậy nên số các số tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị là
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 ( số )
vậy có tất cả 45 tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

Chứng minh bằng quy nạp đi em
Em tự kiểm tra với trường hợp n=2
Giả sử BĐT đúng với \(n=k\) hay \(u_k< \dfrac{2u_1+3\left(k-1\right)}{2}\)
Ta cần chứng minh: \(u_{k+1}< \dfrac{2u_1+3k}{2}\) hay \(\dfrac{u_k^3+4u_k}{u_k^2+1}< \dfrac{2u_1+3k}{2}\)
Do \(\dfrac{2u_1+3k}{2}=\dfrac{2u_1+3\left(k-1\right)}{2}+\dfrac{3}{2}>u_k+\dfrac{3}{2}\)
Nên ta chỉ cần chứng minh:
\(\dfrac{u_k^3+4u_k}{u_k^2+1}\le u_k+\dfrac{3}{2}\Leftrightarrow\dfrac{3}{2}\left(u_k-1\right)^2\ge0\) (luôn đúng)

+ Trước tiên ta đếm số các số tự nhiên có bốn chữ số khác nhau từ các chữ số đã cho.
Gọi số có 4 chữ số là 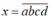
Có 5 cách chọn a(vì a khác 0); khi đó có ![]() cách chọn bcd từ 5 số còn lại.
cách chọn bcd từ 5 số còn lại.
Theo quy tắc nhân có: ![]() số.
số.
+ Tiếp theo, số các số tự nhiên có bốn chữ số khác nhau từ các chữ số đã cho mà không có mặt chữ số 1
Gọi số có 4 chữ số là
Có 4 cách chọn a(vì a khác 0); khi đó có ![]() cách chọn bcd từ 4 số còn lại.
cách chọn bcd từ 4 số còn lại.
Theo quy tắc nhân có ![]() số
số
Vậy số các số tự nhiên có bốn chữ số khác nhau mà nhất thiết phải có mặt số 1 là:
300 – 96 = 204.
Chọn A.

Gọi số tự nhiên cần tìm có dạng \(\overline{abcde}\)
Do a chỉ thuộc {1;2} nên ta chia 2 trường hợp
Trường hợp a=2(b<5):
b có 5 cách chọn
c có 5 cách chọn
d có 4 cách chọn
e có 3 cách chọn
Do đó với trường hợp a=2 ta có: 5.5.4.3=300(cách)
Trường hợp a=1:
b có 6 cách chọn
c có 5 cách chọn
d có 4 cách chọn
e có 3 cách chọn
Do đó trường hợp a=1 có 6.5.4.3=360(cách)
Từ đó để lập được các số tự nhiên thõa đề có: 300+360=660(cách)
Bạn có thể kiểm tra kỹ lại, trong quá trình làm có thể có sai xót về số nhưng hướng làm thì ổn rồi


