Giải hộ em c1 và c3 vs ạ em cảm ơn 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
2
22 tháng 9 2021
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
22 tháng 9 2021
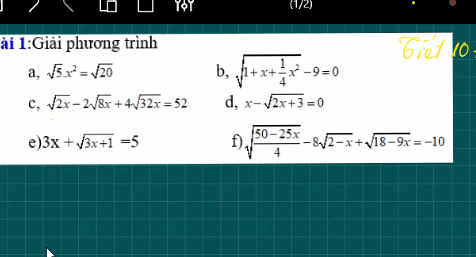
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14
V
1
12 tháng 12 2021
3:
#include <bits/stdc++.h>
using namespace std;
double x,y;
int main()
{
cin>>x>>y;
cout<<fixed<<setprecision(2)<<sqrt(x*x+y*y);
return 0;
}
12 tháng 12 2021
Bn ơi bn viết r chụp lên đc k ạ ? Mik k định dạng đc ý
DT
Đỗ Thanh Hải
CTVVIP
9 tháng 5 2021
1.This work needs…………….by ten today.
A. finish B. finishing C. to finish D. to have finished
Bị động với need thì ta chỉ cần dùng V-ing sau need thôi nhé
LM
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
0
19 tháng 9 2021
\(1,\\ a,ĐK:\left\{{}\begin{matrix}x-2\ne0\\x-2\ge0\end{matrix}\right.\Leftrightarrow x>2\\ b,ĐK:\dfrac{1}{3-2x}\ge0\Leftrightarrow3-2x\ge0\left(1>0\right)\Leftrightarrow x\le\dfrac{3}{2}\)
\(2,\\ a,=\sqrt{\left(6-\sqrt{35}\right)\left(6+\sqrt{35}\right)}=\sqrt{36-35}=\sqrt{1}=1\\ b,=\sqrt{\left(9-\sqrt{17}\right)\left(9+\sqrt{17}\right)}=\sqrt{81-17}=\sqrt{64}=8\\ c,=4\sqrt{2}-6\sqrt{6}+9-4\sqrt{2}+6\sqrt{6}=9\\ d,=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-2-\sqrt{3}=\sqrt{3}+\sqrt{2}-2-\sqrt{3}=\sqrt{2}-2\\ e,=\left(200\sqrt{3}-225\sqrt{3}+25\sqrt{3}\right):\sqrt{15}=0:\sqrt{15}=0\)
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:
Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)
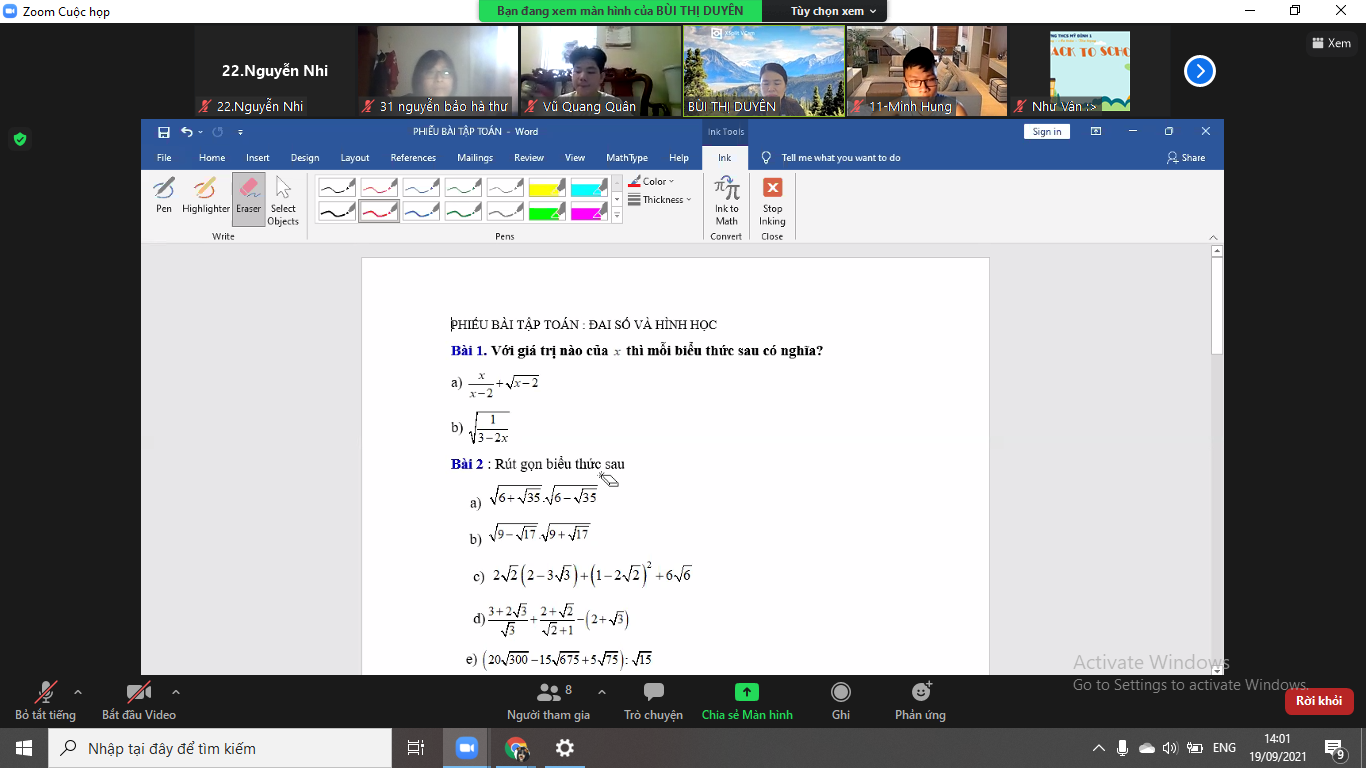
Câu 1:
CaO : oxit bazo
Fe(OH)2: bazo
FeSO4: muối
HCl: axit
NaOH: bazo
Câu 1 phân loại:
Oxit bazơ :CaO
Bazơ: Fe(OH)2, NaOH
Axit:H2SO4, HCl
Muối: FeSO4