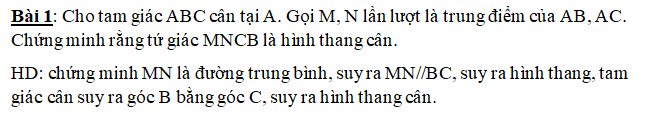Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4
Ta có: \(\left(4+2x\right)\left(4-2x\right)+\left(2x-3\right)^2=2\)
\(\Leftrightarrow16-4x^2+4x^2-12x+9=2\)
\(\Leftrightarrow-12x=-23\)
hay \(x=\dfrac{23}{12}\)

\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)

Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm

Bạn ơi, bạn xem lại đề xem thử có sai ở đâu không nha! Do nếu F nằm trên AD thì làm sao vẽ được góc BFC=90 độ được nhỉ?

Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB

a: Xét tứ giác ABDM có
DM//AB
AM//DB
Do đó: ABDM là hình bình hành
b: Xét ΔCAB và ΔCDB có
CA=CD
BA=BD
CB chung
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}=90^0\)
hay BD⊥DC
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn

 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ