Lý thuyết số là một ngành của toán học lý thuyết nghiên cứu về tính chất của số nói chung và số nguyên nói riêng, cũng như những lớp rộng hơn các bài toán mà phát triển từ những nghiên cứu của nó.
Lý thuyết số có thể chia thành một vài lĩnh vực dựa theo phương pháp giải và các dạng bài toán được xem xét. (Xem Danh sách các chủ đề của lý thuyết số).
Cụm từ "số học" cũng được sử dụng để nói đến lý thuyết số. Đây là cụm từ không còn được sử dụng rộng rãi nữa. Tuy nhiên, nó vẫn còn hiện diện trong tên của một số lĩnh vực toán học (hàm số học, số học đường cong elliptic, lý thuyết căn bản của số học). Việc sử dụng cụm từ số học ở đây không nên nhầm lẫn với số học sơ cấp.
Mục lục
1Các lĩnh vực
1.1Lý thuyết số sơ cấp
1.2Lý thuyết số giải tích
1.3Lý thuyết số đại số
1.4Lý thuyết số hình học
1.5Lý thuyết số tổ hợp
1.6Lý thuyết số máy tính
2Lịch sử
2.1Lý thuyết số thời kì Vedic
2.2Lý thuyết số của người Jaina
2.3Lý thuyết số Hellenistic
2.4Lý thuyết số Ấn Độ cổ điển
2.5Lý thuyết số của người Hồi giáo
2.6Lý thuyết số châu Âu ban đầu
2.7Mở đầu lý thuyết số hiện đại
2.8Lý thuyết số về số nguyên tố
2.9Các thành tựu trong thế kỉ 19
2.10Các thành tựu trong thế kỉ 20
3Danh ngôn
4Tham khảo
5Liên kết ngoài
Các lĩnh vực[sửa | sửa mã nguồn]
Lý thuyết số sơ cấp[sửa | sửa mã nguồn]
Trong lý thuyết số sơ cấp, các số nguyên được nghiên cứu mà không cần các kĩ thuật từ các lĩnh vực khác của toán học. Nó nghiên cứu các vấn đề về chia hết, cách sử dụng thuật toán Euclid để tìm ước chung lớn nhất, phân tích số nguyên thành thừa số nguyên tố, việc nghiên cứu các số hoàn thiện và đồng dư.
Rất nhiều vấn đề trong lý thuyết số có thể phát biểu dưới ngôn ngữ sơ cấp, nhưng chúng cần những nghiên cứu sâu sắc và những tiếp cận mới bên ngoài lĩnh vực lý thuyết số để giải quyết.
Một số ví dụ:
Giả thuyết Goldbach nói về việc biểu diễn các số chẵn thành tổng của hai số nguyên tố.
Giả thuyết Catalan (bây giờ là định lý Mihăilescu) nói về các lũy thừa nguyên liên tiếp.
Giả thuyết số nguyên tố sinh đôi nói rằng có vô hạn số nguyên tố sinh đôi
Giả thuyết Collazt nói về một dãy đệ quy đơn giản
Định lý lớn Fermat (nêu lên vào năm 1637, đến năm 1994 mới được chứng minh) nói rằng phương trình {\displaystyle x^{n}+y^{n}=z^{n}}📷 không có nghiệm nguyên khác không với n lớn hơn 2.
Lý thuyết về phương trình Diophantine thậm chí đã được chứng minh là không có phương pháp chung đề giải (Xem Bài toán thứ 10 của Hilbert)
Lý thuyết số giải tích[sửa | sửa mã nguồn]
Lý thuyết giải tích số sử dụng công cụ giải tích và giải tích phức để giải quyết các vần đề về số nguyên. Định lý số nguyên tố và giả thuyết Riemann là các ví dụ. Bài toán Waring(biểu diễn một số nguyên cho trước thành tổng các bình phương, lập phương, v.v...), giả thuyết số nguyên tố sinh đôi và giả thuyết Goldbach cũng đang bị tấn công bởi các phương pháp giải tích. Chứng minh về tính siêu việt của các hằng số toán học, như là π hay e, cũng được xếp vào lĩnh vực lý thuyết giải tích số. Trong khi những phát biểu về các số siêu việt dường như đã bị loại bỏ khỏi việc nghiên cứu về các số nguyên, chúng thực sự nghiên cứu giá trị của các đa thức với hệ số nguyên tại, ví dụ, e; chúng cũng liên quan mật thiết với lĩnh vực xấp xỉ Diophantine, lĩnh vực nghiên cứu một số thực cho trước có thể xấp xỉ bởi một số hữu tỉ tốt tới mức nào.
Lý thuyết số đại số[sửa | sửa mã nguồn]
Trong Lý thuyết số đại số, khái niệm của một số được mở rộng thành các số đại số, tức là các nghiệm của các đa thức với hệ số nguyên. Những thứ này bao gồm những thành phần tương tự với các số nguyên, còn gọi là số nguyên đại số. Với khái niệm này, những tính chất quen thuộc của số nguyên (như phân tích nguyên tố duy nhất) không còn đúng. Lợi thế của những công cụ lý thuyết - Lý thuyết Galois, group cohomology, class field theory, biểu diễn nhóm và hàm L - là nó cho phép lấy lại phần nào trật tự của lớp số mới.
Rất nhiều vấn đề lý thuyết số có thể được giải quyết một cách tốt nhất bởi nghiên cứu chúng theo modulo p với mọi số nguyên tố p (xem các trường hữu hạn). Đây được gọi là địa phương hóa và nó dẫn đến việc xây dựng các số p-adic; lĩnh vực nghiên cứu này được gọi là giải tích địa phương và nó bắt nguồn từ lý thuyết số đại sô.
Lý thuyết số hình học[sửa | sửa mã nguồn]
Lý thuyết số hình học (cách gọi truyền thống là (hình học của các số) kết hợp tất cả các dạng hình học. Nó bắt đầu với định lý Minkowski về các điểm nguyên trong các tập lồi và những nghiên cứu về sphere packing.
Lý thuyết số tổ hợp[sửa | sửa mã nguồn]
Lý thuyết số tổ hợp giải quyết các bài toán về lý thuyết số mà có tư tưởng tổ hợp trong công thức hoặc cách chứng minh của nó. Paul Erdős là người khởi xướng chính của ngành lý thuyết số này. Những chủ đề thông thường bao gồm hệ bao, bài toán tổng-zero, rất nhiều restricted sumset và cấp số cộng trong một tập số nguyên. Các phương pháp đại số hoặc giải tích rất mạnh trong những lĩnh vực này.
Lý thuyết số máy tính[sửa | sửa mã nguồn]
Lý thuyết số máy tính nghiên cứu các thuật toán liên quan đến lý thuyết số. Những thuật toán nhanh chóng để kiểm tra tính nguyên tố và phân tích thừa số nguyên tố có những ứng dụng quan trọng trong mã hóa.
Lịch sử[sửa | sửa mã nguồn]
Lý thuyết số thời kì Vedic[sửa | sửa mã nguồn]
Các nhà toán học Ấn Độ đã quan tâm đến việc tìm nghiệm nguyên của phương trình Diophantine từ thời kì Vedic. Những ứng dụng sớm nhất vào hình học của phương trình Diophantine có thể tìm thấy trong kinh Sulba, được viết vào khoảng giữa thế kỉ thứ 8 và thế kỉ thứ 6 trước Công nguyên. Baudhayana (năm 800 TCN) tìm thấy hai tập nghiệm nguyên dương của một hệ các phương trình Diophantine, và cũng sử dụng hệ phương trình Diophantine với tới bốn ẩn. Apastamba (năm 600) sử dụng hệ phương trình Diophantine với tới năm ẩn.
Lý thuyết số của người Jaina[sửa | sửa mã nguồn]
Ở Ấn Độ, các nhà toán học Jaina đã phát triển lý thuyết số có hệ thống đầu tiên từ thế kỉ thứ 4 trước Công Nguyên tới thế kỉ thứ 2. Văn tự Surya Prajinapti (năm 400 TCN) phân lớp tất cả các số thành ba tập: đếm được, không đếm được và vô hạn. Mỗi tập này lại được phân thành ba cấp:
Đếm được: thấp nhất, trung bình, và cao nhất.
Không đếm được: gần như không đếm được, thật sự không đếm được, và không đếm được một cách không đếm được.
Vô hạn: gần như vô hạn, thật sự vô hạn, vô hạn một cách vô hạn
Những người Jain là những người đầu tiên không chấp nhận ý tưởng các vô hạn đều như nhau. Họ nhận ra năm loại vô hạn khác nhau: vô hạn theo một hoặc hai hướng (một chiều), vô hạn theo diện tích (hai chiều), vô hạn mọi nơi (ba chiều), và vô hạn liên tục (vô số chiều).
Số đếm được cao nhất N của người Jain tương ứng với khái niệm hiện đại aleph-không {\displaystyle \aleph _{0}}📷 (cardinal number của tập vô hạn các số nguyên 1,2,...), the smallest cardinal transfinite number. Người Jain cũng định nghĩa toàn bộ hệ thống các cardinal number, trong đó {\displaystyle \aleph _{0}}📷 là nhỏ nhất.
Trong công trình của người Jain về lý thuyết tập hợp, họ phân biệt hai loại transfinite number cơ bản. Ở cả lĩnh vực vật lý và bản thể học (ontology), sự khác nhau được tạo ra giữa asmkhyata và ananata, giữa vô hạn bị chặn ngặt và vô hạn bị chặn lỏng.
Lý thuyết số Hellenistic[sửa | sửa mã nguồn]
Lý thuyết số là một đề tài ưa thích của các nhà toán học Hellenistic ở Alexandria, Ai Cập từ thế kỉ thứ 3 sau Công Nguyên. Họ đã nhận thức được khái niệm phương trình Diophantine trong rất nhiều trường hợp đặc biệt. Nhà toán học Hellenistic đầu tiên nghiên cứu những phương trình này là Diophantus.
Diophantus cũng đã tìm kiếm một phương pháp để tìm nghiệm nguyên của các phương trình vô định tuyến tính, những phương trình mà thiếu điều kiện đủ để có một tập duy nhất các nghiệm phân biệt. Phương trình {\displaystyle x+y=5}📷 là một phương trình như vậy. Diophantus đã khám phá ra nhiều phương trình vô định có thể biến đổi thành các dạng đã biết mặc dù thậm chí còn không biết được nghiệm cụ thể.
Lý thuyết số Ấn Độ cổ điển[sửa | sửa mã nguồn]
Phương trình Diophantine đã được nghiên cứu một cách sâu sắc bởi các nhà toán học Ân Độ trung cổ. Họ là những người đầu tiên nghiên cứu một cách có hệ thống các phương pháp tìm nghiệm nguyên của phương trình Diophantine. Aryabhata (499) là người đầu tiên tìm ra dạng nghiệm tổng quát của phương trình Diophantine tuyến tính {\displaystyle ay+bx=c}📷, được ghi trong cuốn Aryabhatiya của ông. Thuật toán kuttaka này được xem là một trong những cống hiến quan trọng nhất của Aryabhata trong toán học lý thuyết, đó là tìm nghiệm của phương trình Diophantine bằng liên phân số. Aryabhata đã dùng kĩ thuật này để tìm nghiệm nguyên của các hệ phương trình Diophantine, một bài toán có ứng dụng quan trọng trong thiên văn học. Ông cũng đã tìm ra nghiệm tổng quát đối với phương trình tuyến tính vô định bằng phương pháp này.
Brahmagupta vào năm 628 đã nắm được những phương trình Diophantine phức tạp hơn. Ông sử dụng phương pháp chakravala để giải phương trình Diophantine bậc hai, bao gồm cả các dạng của phương trình Pell, như là {\displaystyle 61x^{2}+1=y^{2}}📷. Cuốn Brahma Sphuta Siddhanta của ông đã được dịch sang tiếng Ả Rập vào năm 773 và sau đó được dịch sang tiếng Latin vào năm 1126. Phương trình {\displaystyle 61x^{2}+1=y^{2}}📷 sau đó đã được chuyển thành một bài toán vào năm 1657 bởi nhà toán học người Pháp Pierre de Fermat. Leonhard Euler hơn 70 năm sau đã tìm được nghiệm tổng quát đối với trường hợp riêng này của phương trình Pell, trong khi nghiệm tổng quát của phương trình Pell đã được tìm ra hơn 100 năm sau đó bởi Joseph Louis Lagrange vào 1767. Trong khi đó, nhiều thế kỉ trước, nghiệm tổng quát của phương trình Pell đã được ghi lại bởi Bhaskara II vào 1150, sử dụng một dạng khác của phương pháp chakravala. Ông cũng đã sử dụng nó để tìm ra nghiệm tổng quát đối với các phương trình vô định bậc hai và phương trình Diophantine bậc hai khác. Phương pháp chakravala của Bhaskara dùng để tìm nghiệm phương trình Pell đơn giản hơn nhiều so với phương pháp mà Lagrange sử dụng 600 năm sau đó. Bhaskara cũng đã tìm được nghiệm của các phương trình vô định bậc hai, bậc ba, bốn và cao hơn. Narayana Pandit đã cải tiến phương pháp chakravala và tìm thêm được các nghiệm tổng quát hơn đối với các phương trình vô định bậc hai và cao hơn khác.
Lý thuyết số của người Hồi giáo[sửa | sửa mã nguồn]
Từ thế kỉ 9, các nhà toán học Hồi giáo đã rất quan tâm đến lý thuyết số. Một trong những nhà toán học đầu tiên này là nhà toán học Ả Rập Thabit ibn Qurra, người đã khám phá ra một định lý cho phép tìm các cặp số bạn bè, tức là các số mà tổng các ước thực sự của số này bằng số kia. Vào thế kỉ 10, Al-Baghdadi đã nhìn vào một ít biến đổi trong định lý của Thabit ibn Qurra.
Vào thế kỉ 10, al-Haitham có thể là người đầu tiên phân loại các số hoàn hảo chẵn (là các số mà tổng các ước thực sự của nó bằng chính nó) thành các số có dạng {\displaystyle 2^{k-1}(2^{k}-1)}📷trong đó {\displaystyle 2^{k}-1}📷 là số nguyên tố. Al-Haytham cũng là người đầu tiên phát biểu định lý Wilson (nói rằng p là số nguyên tố thì {\displaystyle 1+(p-1)!}📷 chia hết cho p). Hiện không rõ ông ta có biết cách chứng minh nó không. Định lý có tên là định lý Wilson vì căn cứ theo một lời chú thích của Edward Waring vào năm 1770 rằng John Wilson là người đầu tiên chú ý đến kết quả này. Không có bằng chứng nào chứng tỏ John Wilson đã biết cách chứng minh và gần như hiển nhiên là Waring cũng không. Lagrange đã đưa ra chứng minh đầu tiên vào 1771.
Các số bạn bè đóng vai trò quan trọng trong toán học của người Hồi giáo. Vào thế kỉ 13, nhà toán học Ba Tư Al-Farisi đã đưa ra một chứng minh mới cho định lý của Thabit ibn Qurra, giới thiệu một ý tưởng mới rất quan trọng liên quan đến phương pháp phân tích thừa số và tổ hợp. Ông cũng đưa ra cặp số bạn bè 17296, 18416 mà người ta vẫn cho là của Euler, nhưng chúng tao biết rằng những số này còn được biết đến sớm hơn cả al-Farisi, có thể bởi chính Thabit ibn Qurra. Vào thế kỉ 17, Muhammad Baqir Yazdi đưa ra cặp số bạn bè 9.363.584 và 9.437.056 rất nhiều năm trước khi Euler đưa ra.
Lý thuyết số châu Âu ban đầu[sửa | sửa mã nguồn]
Lý thuyết số bắt đầu ở Châu Âu vào thế kỉ 16 và 17, với François Viète, Bachet de Meziriac, và đặc biệt là Fermat, mà phương pháp lùi vô hạn của ông là chứng minh tổng quát đầu tiên của phương trình Diophantine. Định lý lớn Fermat được nêu lên như là một bài toán vào năm 1637, và không có lời giải cho đến năm 1994. Fermat cũng nêu lên bài toán {\displaystyle 61x^{2}+1=y^{2}}📷 vào năm 1657.
Vào thế kỉ 18, Euler và Lagrange đã có những cống hiến quan trọng cho lý thuyết số. Euler đã làm một vài công trình về lý thuyết giải tích số, và tình được một nghiệm tổng quát của phương trình {\displaystyle 61x^{2}+1=y^{2}}📷, mà Fermat nêu thành bài toán. Lagrange đã tìm được một nghiệm của phương trình Pell tổng quát hơn. Euler và Lagrange đã giải những phương trình Pell này bằng phương pháp liên phân số, mặc dù nó còn khó hơn phương pháp chakravala của Ấn Độ.
Mở đầu lý thuyết số hiện đại[sửa | sửa mã nguồn]
Khoảng đầu thế kỉ 19 các cuốn sách của Legendre (1798), và Gauss kết hợp thành những lý thuyết có hệ thống đầu tiên ở châu Âu. Cuốn Disquisitiones Arithmeticae (1801) có thể nói là đã mở đầu lý thuyết số hiện đại.
Sự hình thành lý thuyết đồng dư bắt đầu với cuốn Disquisitiones của Gauss. Ông giới thiệu ký hiệu
{\displaystyle a\equiv b{\pmod {c}},}📷
và đã khám phá ra hầu hết trong lĩnh vực này. Chebyshev đã xuất bản vào năm 1847 một công trình bằng tiếng Nga về chủ đề này, và ở Pháp Serret đã phổ biến nó.
Bên cạnh những công trình tổng kết trước đó, Legendre đã phát biểu luật tương hỗ bậc hai. Định lý này, được khám phá ra bởi qui nạp và được diễn đạt bởi Euler, đã được chứng minh lần đầu tiên bởi Legendre trong cuốn Théorie des Nombres của ông (1798) trong những trường hợp đặc biệt. Độc lập với Euler và Legendre, Gauss đã khám phá ra định luật này vào khoảng năm 1795, và là người đầu tiên đưa ra chứng minh tổng quát. Những người cũng có cống hiến quan trọng: Cauchy; Dirichlet với cuốn Vorlesungen über Zahlentheorie kinh điển; Jacobi, người đã đưa ra ký hiệu Jacobi; Liouville, Zeller (?), Eisenstein, Kummer, và Kronecker. Lý thuyết này đã được mở rộng để bao gồm biquadratic reciprocity (Gauss, Jacobi những người đầu tiên chứng minh luật tương hỗ bậc ba, và Kummer).
Gauss cũng đã đưa ra biểu diễn các số thành các dạng bậc hai cơ số hai.
Lý thuyết số về số nguyên tố[sửa | sửa mã nguồn]
Một chủ đề lớn và lặp đi lặp lại trong lý thuyết số đó là nghiên cứu về sự phân bố số nguyên tố. Carl Fiedrich Gauss đã dự đoán kết quả của định lý số nguyên tố khi còn là học sinh trung học.
Chebyshev (1850) đưa ra các chặn cho số số nguyên tố giữa hai giới hạn cho trước. Riemann giới thiệu giải tích phức thành lý thuyết về hàm zeta Riemann. Điều này đã dẫn đến mối quan hệ giữa các số không của hàm zeta và sự phân bố số nguyên tố, thậm chí dẫn tới một chứng minh cho định lý số về số nguyên tố độc lập với Hadamard và de la Vallée Poussin vào năm 1896. Tuy nhiên, một chứng minh sơ cấp đã được đưa ra sau đó bởi Paul Erdős và Atle Selberg vào năm 1949. Ở đây sơ cấp nghĩa là không sử dụng kĩ thuật giải tích phức; tuy nhiên chứng minh vẫn rất đặc biệt và rất khó. Giả thuyết Riemann, đưa ra những thông tin chính xác hơn, vẫn còn là một câu hỏi mở.
Các thành tựu trong thế kỉ 19[sửa | sửa mã nguồn]
Cauchy, Pointsot (1845), Lebesgue (1859, 1868) và đặc biệt là Hermite đã có những cống hiến đối với lĩnh vực này. Trong lý thuyết về các ternary form Eisenstein đã trở thành người đi đầu, và với ông và H. J. S. Smith đó đúng là một bước tiến quan trọng trong lý thuyết về các dạng. Smith đã đưa ra một sự phân loại hoàn chỉnh về các ternary form bậc hai, và mở rộng những nghiên cứu của Gauss về các dạng bậc hai thực (real quadratic form) thành các dạng phức (complex form). Những nghiên cứu về biểu diễn các số thành tổng của 4, 5, 6, 6, 8 bình phương đã được phát triển bởi Eisenstein và lý thuyết này đã được hoàn chỉnh bởi Smith.
Dirichlet là người đầu tiên thuyết trình về lĩnh vực này ở một trường đại học ở Đức. Một trong những cống hiến của ông là sự mở rộng của Định lý lớn Fermat:
{\displaystyle x^{n}+y^{n}\neq z^{n},(x,y,z\neq 0,n>2)}📷
mà Euler và Legendre đã chứng minh cho n = 3, 4 (và từ đó suy ra cho các bội của 3 và 4). Dirichlet đã chỉ ra rằng:{\displaystyle x^{5}+y^{5}\neq az^{5}}📷. Một số nhà toán học Pháp là Borel, Poincaré, những hồi ký của họ rất lớn và có giá trị; Tannery và Stieltjes. Một số người có những cống hiến hàng đầu ở Đức là Kronecker, Kummer, Schering, Bachmann, và Dedekind. Ở Austria cuốn Vorlesungen über allgemeine Arithmetik của Stolz (1885-86) và ở Anh cuốn Lý thuyết số của Mathew (Phần I, 1892) là các công trình tổng quát rất có giá trị. Genocchi, Sylvester, và J. W. L. Glaisher cũng đã có những cống hiến cho lý thuyết này.
Các thành tựu trong thế kỉ 20[sửa | sửa mã nguồn]
Những nhà toán học lớn trong lý thuyết số thế kỉ 20 bao gồm Paul Erdős, Gerd Faltings, G. H. Hardy, Edmund Landau, John Edensor Littlewood, Srinivasa Ramanujan và André Weil.
Các cột mốc trong lý thuyết số thế kỉ 20 bao gồm việc chứng minh Định lý lớn Fermat bởi Andrew Wiles vào năm 1994 và chứng minh Giả thuyết Taniyama–Shimura vào năm 1999
Danh ngôn[sửa | sửa mã nguồn]
Toán học là nữ hoàng của các khoa học và lý thuyết số là nữ hoàng của toán học. — Gauss
Chúa sinh ra các số nguyên, và phần việc còn lại là của con người. — Kronecker
Tôi biết các con số rất đẹp đẽ. Nếu chúng không đẹp, thì chẳng có thứ gì đẹp.— Erdős
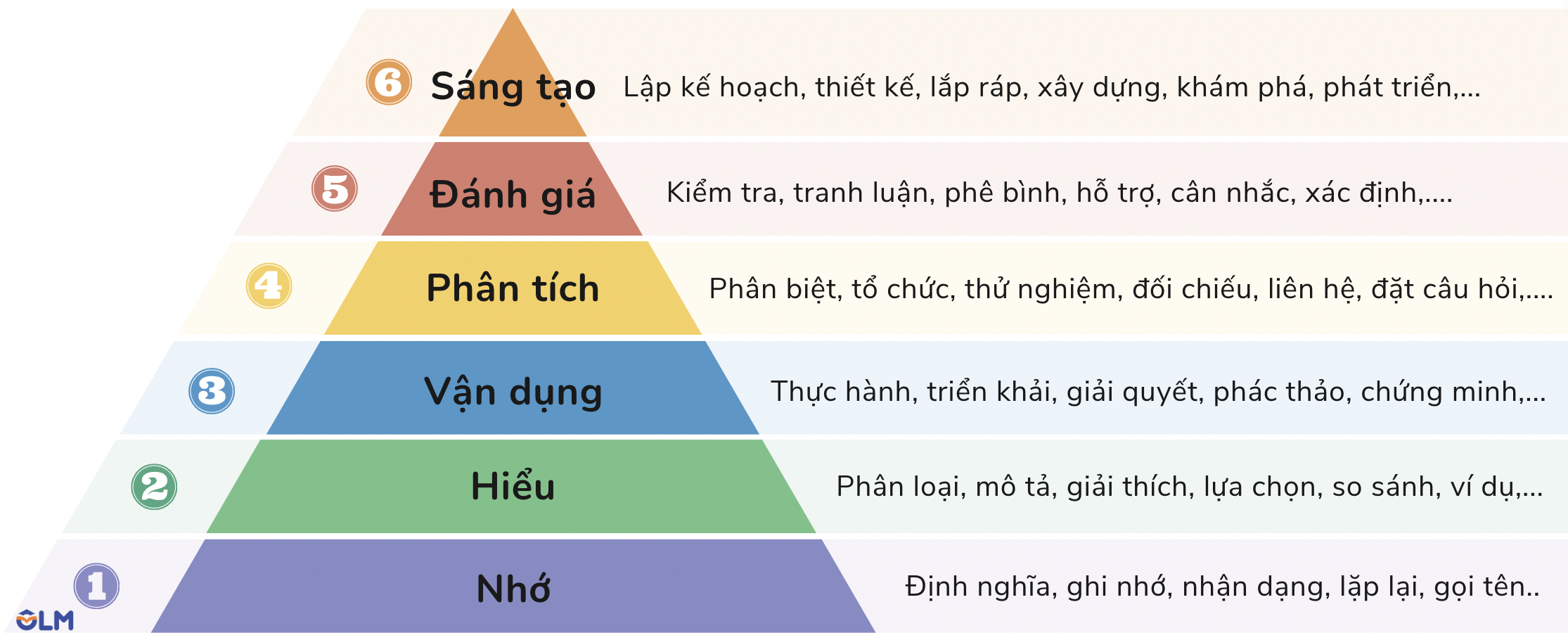


em thấy mik mới đc ở bậc 3
Thật ra là các bạn c2 đã đủ khả năng ở 6 bậc rồi, nhưng mà nó ít hay nhiều thôi í