giup minh cau nay voi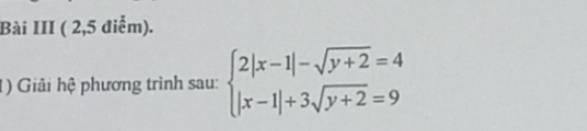
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TP
0
Giúp mình câu này với ! với giải thichs giúp mình nhe!^^
10 tháng 12 2021
= 154 . 235 + 154 . (-35)
= 154 . [ 235 + (-35)]
= 154 . 200
= 30800
VV
0
18 tháng 10 2021
a: Ta có: A và E đối xứng nhau qua Ox
nên OA=OE(1)
Ta có: A và B đối xứng nhau qua Oy
nên OA=OB(2)
Từ (1) và (2) suy ra OE=OB
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
TP
Thảo Phương
CTVVIP
21 tháng 7 2021
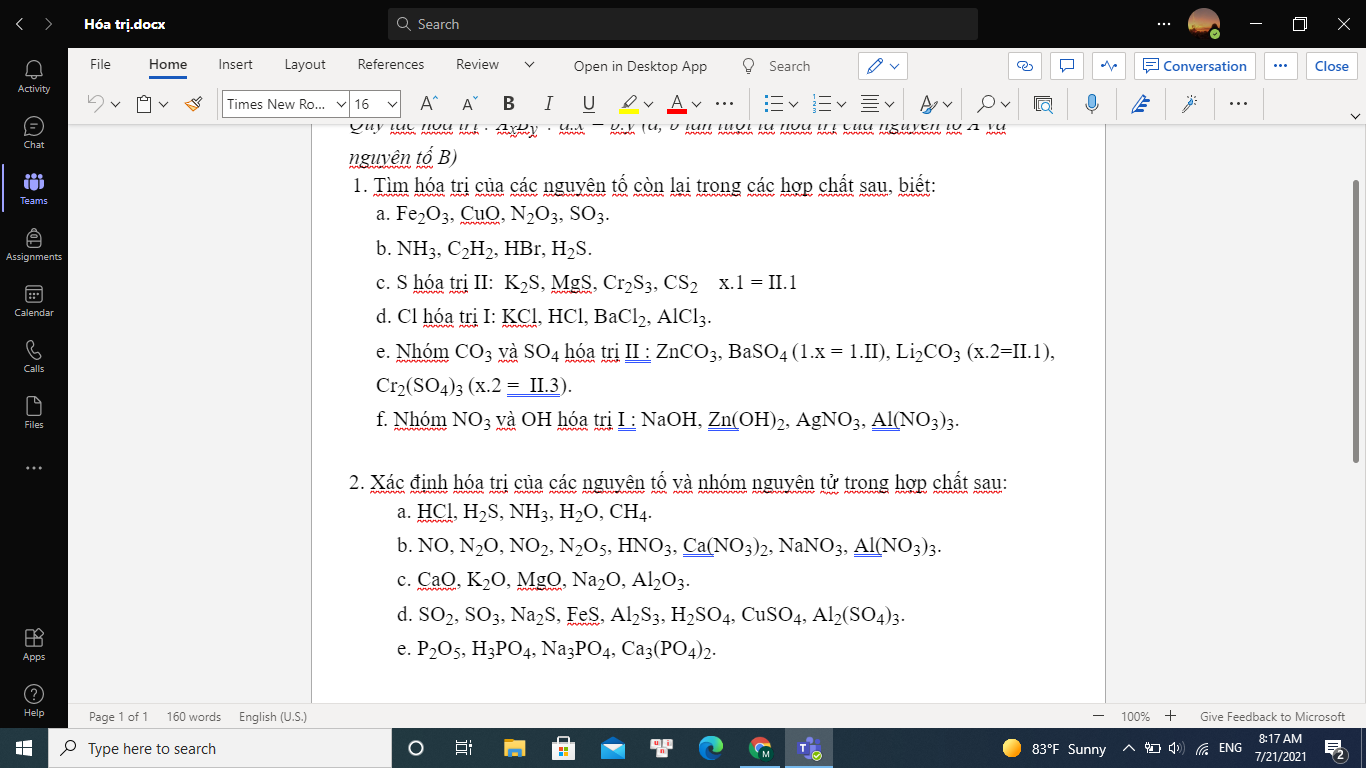
1/ Gọi x là hóa trị của nguyên tố cần tìm. Áp dụng quy tắc hóa trị:
a) Fe2O3 : x.2=II.3 => x=III
CuO : x.1=II.1 => x=II
N2O3 : x.2=II.3 => x=III
SO3: x.1=II.3 => x= VI
b) NH3 : x.1=I.3 => x=III
C2H2 : C hóa trị IV, H hóa trị I ( do trong hợp chất hữu cơ, hóa trị của C luôn là IV)
HBr : I.1=x.1 => x=I
H2S: I.2=x.1 => x=II
c)K2S: x.2=II.1 => x=I
MgS : x.1=II.1 => x=II
Cr2S3 : x.2=II.3 => x=III
CS2: x.1=II.2=> x=IV
d) KCl: x.1=I.1=> x=I
HCl: x.1= 1.I => x=I
BaCl2 : x.1=I.2 => x=II
AlCl3 : x.1=I.3 => x=III
e) ZnCO3 : x.2=II.1 => x=II
BaSO4 : x.1=II.1 => x=II
Li2CO3 : x.2=II.1 => x=I
Cr2(SO4)3 : x.2=II.3 => x=III
f) NaOH : x.1=1.I => x=I
Zn(OH)2 : x.1=I.2 => x=II
AgNO3 : x.1=I.1 => x=I
Al(NO3)3 : x.1=I.3 => x=III
TP
Thảo Phương
CTVVIP
21 tháng 7 2021
2.a) HCl : H(I), Cl(I)
H2S: H(I), S(II)
NH3 : N(III), H(I)
H2O : H(I), O(II)
CH4: C(IV), H(I)
b) NO: N(II), O(II)
N2O: N(I), O(II)
NO2: N(IV), O(II)
N2O5: N(V), O(II)
HNO3 : H(I), NO3 (I)
Ca(NO3)2 : Ca(II), NO3 (I)
NaNO3: Na(I), NO3 (I)
Al(NO3)3: Al (III),NO3 (I)
c) CaO: Ca(II), O(II)
K2O: K(I), O(II)
MgO : Mg(II), O(II)
Na2O: Na(I), O(II)
Al2O3: Al(III), O(II)
d) SO2: S(IV) ,O(II)
SO3: S(VI), O(II)
Na2S: Na(I), S(II)
FeS: Fe(II), S(II)
Al2S3: Al(III), S(II)
H2SO4: H(I), SO4(II)
CuSO4: Cu(II), SO4(II)
Al2(SO4)3: Al(III), SO4(II)
e) P2O5: P(V), O(II)
H3PO4: H(I), PO4(III)
Na3PO4: Na(I), PO4(III)
Ca3(PO4)2: Ca(II), PO4(III)
8 tháng 3 2022
uses crt;
var st:string;
d,i:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do
if (st[i] in ['0'..'9']) then write(st[i]);
readln;
end.
U
1
8 tháng 6 2021
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
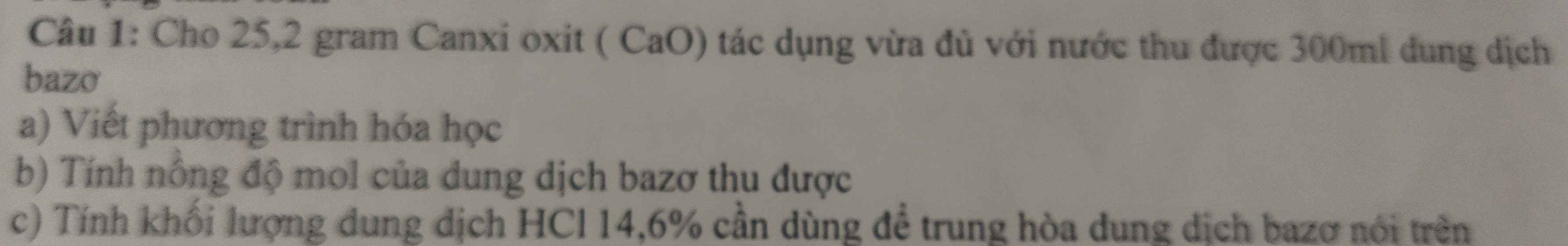
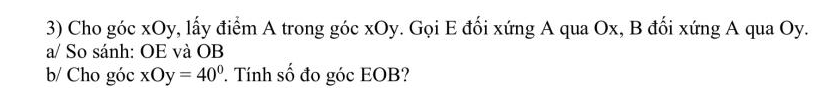
Đặt \(\left\{{}\begin{matrix}a=\left|x-1\right|\\b=\sqrt{y+2}\left(b>0\right)\end{matrix}\right.\)
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2a-b=4\\a+3b=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2a-4\\a+3.\left(2a-4\right)=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2a-4\\7a-12=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2a-4\\a=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x-1\right|=3\\\sqrt{y+2}=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\\y=2\end{matrix}\right.\)
Vây...
Thầy ơi thầy nhầm rồi ạ đề bài yêu cầu là: \(\left|x-1\right|+3\sqrt{y+2}=9\)