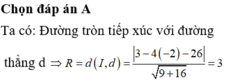Trên mặt phẳng tọa độ Oxy, cho đường thẳng \(d:2x+4y+1=0\) . Đường thẳng d' song song với đường thẳng d và tạo với tia Ox, Oy một tam giác có diện tích bằng 1. Tìm pt tổng quát của đường thẳng d'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
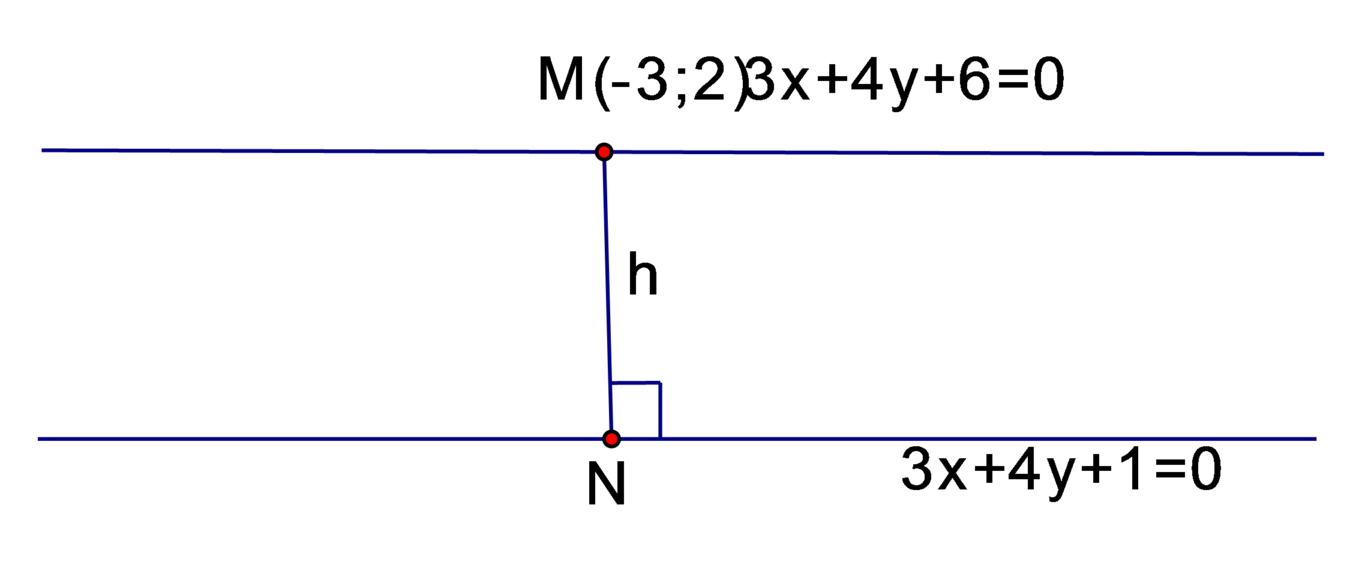
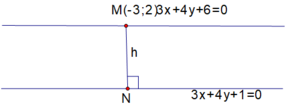
Độ dài véc tơ v → bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó: v → = M N →
Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:
M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3
⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5
⇒ M N → = − 3 5 ; − 4 5

a: Vì (d)//x-4y+5=0 nên (d): x-4y+c=0
Thay x=1 và y=0 vào (d), ta được:
c+1=0
=>c=-1
=>x-4y-1=0
b: Vì (d) vuông góc x-4y+5=0
nên (d): 4x+y+c=0
Thay x=1 và y=0 vào (d), ta được:
c+4=0
=>c=-4
=>4x+y-4=0

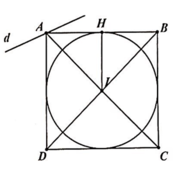
b) Xét tam giác OMB vuông tại O có:
BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2
Tương tự tam giác OAB vuông tại O có:
B A 2 = O A 2 + O B 2 = 1 + 1 = 2 ⇒ BA = 2
Xét tam giác MAB có:
B M 2 + B A 2 = 2 + 2 = 4 = A M 2
⇒ ΔMAB vuông tại B
Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = 2

Gọi đt ( d) là\(ax+by=0\)(*)
+ Vì đt (d) qua M nên: x=1 và y=3 thay vào(*) có:\(a+3y=0\) (**)
+ Vì đt (d) song song với đt (◇) nên \(a//6\) và \(b=-4\) thay vào (**) có:
\(a+3\left(-4\right)=0\)
\(\rightarrow a=12\)
Vậy đt (d) có dạng \(12x+3y=0\)
ta có phương trình \(\left(\Delta\right)\) <=> \(y=\frac{3}{2}x+\frac{1}{4}\)
vì (d) //\(\left(\Delta\right)\) --> \(\left(\Delta\right)y=\frac{3}{2}x+b\) điều kiện là \(b\ne\frac{1}{4}\)
vì (d) qua M nên \(3=\frac{3}{2}+b\Leftrightarrow b=\frac{3}{2}\)
\(\Rightarrow\left(\Delta\right)y=\frac{3}{2}x+\frac{3}{2}\Leftrightarrow3x-2y+3=0\)
vậy \(\left(\Delta\right)3x-2y+3=0\)