cho tam giác ABC vuông tại A có AB=12.Trên AB lấy M sao cho AM=3 kẻ MN vuông góc với AB (N thuộc BC) biết MN =15 .Vậy AC=?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2023
a: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>AM=AN
b: Xét ΔACB có AM/AB=AN/AC
nên MN//BC
c: Xét ΔADE có
AM vừa là đường cao, vừa là trung tuýen
=>ΔADE cân tại A
=>AD=AE
Xét ΔADF có
AN vừa là đường cao, vừa là trung tuyến
=>ΔADF cân tại A
=>AD=AF
=>AE=AF
=>ΔAEFcân tạiA
17 tháng 1 2021
Sửa đề: N∈BC
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
M∈AB(gt)
N∈BC(gt)
MN//BC(gt)
Do đó: \(\dfrac{NC}{BC}=\dfrac{AM}{AB}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{NC}{10}=\dfrac{4}{6}=\dfrac{2}{3}\)
hay \(NC=\dfrac{20}{3}cm\)
Ta có: NC+NB=BC(N nằm giữa B và C)
hay \(NB=BC-NC=10-\dfrac{20}{3}=\dfrac{10}{3}cm\)
Xét ΔABC có
N∈BC(gt)
M∈AB(gt)
MN//AC(gt)
Do đó: \(\dfrac{MN}{AC}=\dfrac{BN}{BC}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{8}=\dfrac{10}{3}:10\)
\(\Leftrightarrow MN=\dfrac{10}{3}\cdot\dfrac{1}{10}\cdot8\)
hay \(MN=\dfrac{8}{3}cm\)
Vậy: \(NC=\dfrac{20}{3}cm\); \(MN=\dfrac{8}{3}cm\)
CM
28 tháng 4 2017
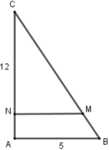
Tam giác ABC vuông tại A, theo định lí Pi-ta-go ta có:
B C 2 = A B 2 + A C 2 ⇒ B C 2 = 5 2 + 12 2 = 169 ⇒ B C = 13
BM = 5 13 BC = 5 13 .13 = 5 => CM = 13 - 5 = 8.
Xét ΔCMN và ΔCBA có:
N = A = 90 ∘ (gt)
Góc C chung
=> ΔCMN ~ ΔCBA (g - g) => (cạnh tương ứng)
⇒ M N = A B . C M C B = 5.8 13 = 40 13
Đáp án: C
30 tháng 3 2023
ta có diện tích tam giác ABC là
AB x AC : 2 = 12 x18 : 2 = 108 cm2
diện tích tam giác ABC bằng tổng diện tích tam giác BMN và diện tích hình thang AMNC , ta có
BM x MN : 2 + (MN + AC) x AM : 2 = 108
8 x MN: 2 + (MN +18 ) x 4 : = 108
6 x MN =72
MN =12
vậy MN =12 cm
BM=AB-AM=12-3=9
ta có
BA vuông góc AC
BA vuông góc MN
=>AC//MN
áp dụng hệ quả của te-lét ta đc
BM/BA=MN/AC
=>9/12=15/AC
=>15.12/9=AC
=>AC=180/9=20