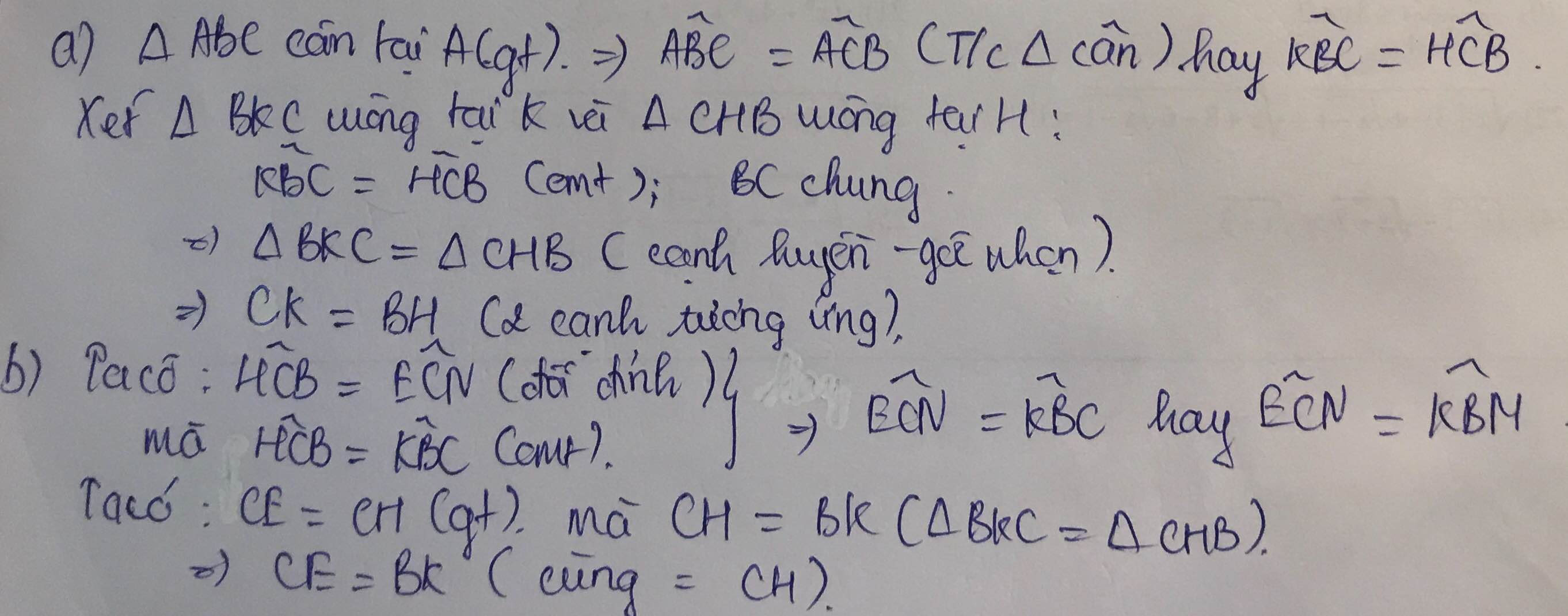Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
hay ΔAMN cân tại A
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
c: Ta có: ΔABH=ΔACK
nên AH=AK
d: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN
\(\widehat{M}=\widehat{N}\)
Do đó: ΔHBM=ΔKCN
Suy ra: \(\widehat{HBM}=\widehat{KCN}\)
mà \(\widehat{HBM}=\widehat{OBC}\)
và \(\widehat{KCN}=\widehat{OCB}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O

a) △ABC cân ⇒ \(\widehat{ABC}=\widehat{ACB}\) ⇒\(\widehat{ABM}=\widehat{ACN}\)
Xét △ABM và △ACN có:
\(AB=AC\) ( Vì △ABC cân)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
BM=CN(gt)
Do đó : △ABC=△ACN\(\left(c.g.c\right)\)
b)Xét △vuoongAHB và △vuoongAKC có
AB=AC(vì △ABC cân)
\(\widehat{HAB}=\widehat{KAC}\) (vì △ABM=△ACN)
⇒△AHB=△AKC ( cạnh huyền góc nhọn)
⇒AH=AK
a, Ta có : ^ABM = ^MBC - ^ABC (1)
^ACN = ^NCB - ^ACB (2)
Từ (1) ; (2) suy ra ^ABM = ^ACN
Xét tam giác ABM và tam giác ANC có :
^ABM = ^ANC ( cmt )
AB = AC ( gt )
MB = NC (gt)
Vậy tam giác ABM = tam giác ACN ( c.g.c )
=> AM = AN ( 2 cạnh tương ứng )
Xét tam giác AMN có : AN = AM
Vậy tam giác AMN là tam giác cân tại A
=> ^M = ^N (3)
b, Ta có : ^AMB = ^ABH ( cùng phụ ^HBM ) (4)
^ACK = ^ANC ( cùng phụ ^KCN ) (5)
Từ (3) ; (4) ; (5) suy ra : ^ABH = ^ACK
=> ^HBM = ^KCN
Xét tam giác AHB và tam giác AKC ta có :
^ABH = ^ACK ( cmt )
AB = AC
^AHB = ^AKC = 900
Vậy tam giác AHB = tam giác AKC ( ch - gn )
=> AH = AK ( 2 cạnh tương ứng )
c, Ta có : ^HBM = ^OBC ( đối đỉnh )
^KCN = ^BCO ( đối đỉnh )
mà ^HBM = ^KCN (cmt)
Xét tam giác OBC có :
^OBC = ^OCB vậy tam giác OBC cân tại O

a: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>AM=AN
b: Xét ΔACB có AM/AB=AN/AC
nên MN//BC
c: Xét ΔADE có
AM vừa là đường cao, vừa là trung tuýen
=>ΔADE cân tại A
=>AD=AE
Xét ΔADF có
AN vừa là đường cao, vừa là trung tuyến
=>ΔADF cân tại A
=>AD=AF
=>AE=AF
=>ΔAEFcân tạiA

a, Xét tam giác vuông MHC có :
\(\widehat{CMH}+\widehat{HCM}=90^o\)
Xét tam giác vuông ABC có:
\(\widehat{HIB}+\widehat{HCM}=90^o\)
\(\Rightarrow\widehat{CMH}=\widehat{HIB}\)
Xét 2 tam giác : KHM và IHB
MH = HB ( gt )
\(\widehat{CMN}=\widehat{HBI}\left(cmt\right)\)
\(\widehat{MKH}=\widehat{HIB}=90^o\)
\(\Rightarrow\Delta KHM=\Delta IHB\)
b, \(\Rightarrow HK=HI\)
Xét 2 tam giác : KHA và IHA
KM = IH ( cm a )
AN chung
\(\widehat{HKA}=\widehat{AIM}=90^o\)
\(\Rightarrow\Delta KHA=\Delta IHA\)
\(\Rightarrow\widehat{KAH}=\widehat{HAI}\)
Vậy : AH là tia phân giác góc BAC
a, xet △ vuong mhc co ∠cmh + ∠hcm = 90 do xet △ vuong abc co ∠hbi + ∠hcm = 90 do suy ra ∠cmh = ∠hbi xet △ BHI va △ MHK co ∠CMH = ∠HBI [c/m tr] HM = BH [gt] ∠BIH = ∠MKH [=90 do] ➩ △ BHI = △ MHK [ch-gn] b, tu a co △bhi = △mhk ➩ ih = kh xet △aih va △akh co ah chung ih = kh [c/m tr] ∠aih = ∠akh [= 90 do] ➩ △aih = △kah [ch-cgv] ➩ ∠iah = ∠kah ➩ ah la p/g cua ∠bac