Giải chi tiết giúp e câu 14 vs ạ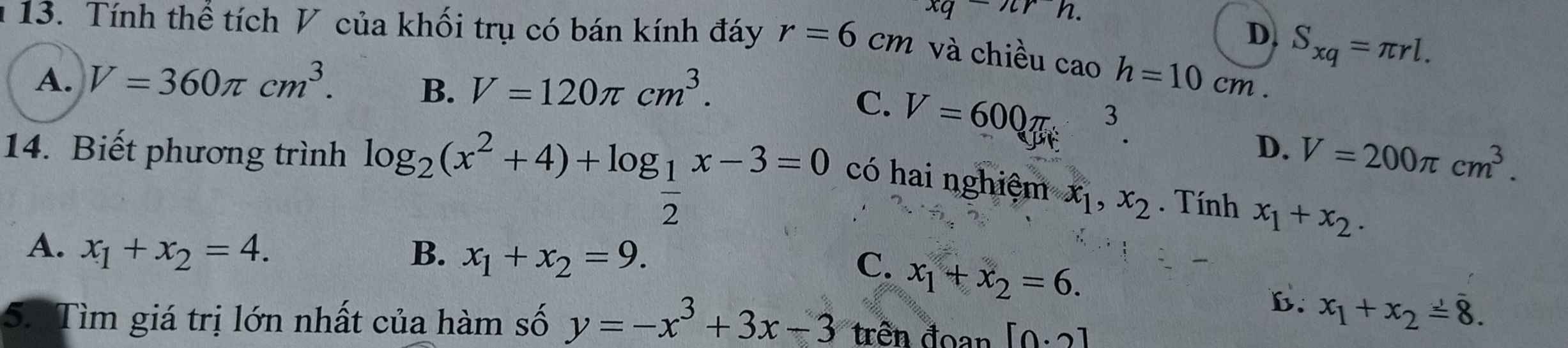
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
\(\begin{array} {l} 13)\\ n_{HCHO}=\dfrac{1,2}{30}=0,04(mol)\\ HCHO\xrightarrow{+AgNO_3/NH_3,t^o}4Ag\\ n_{Ag}=4n_{HCHO}=0,16(mol)\\ m=0,16.108=17,28(g)\\ \to A\\ 14)\\ X:C_nH_{2n}\\ n_{Br_2}=\dfrac{8}{160}=0,05(mol)\\ C_nH_{2n}+Br_2\to C_nH_{2n}Br_2\\ n_{C_nH_{2n}}=n_{Br_2}=0,05(mol)\\ M_{C_nH_{2n}}=14n=\dfrac{1,4}{0,05}=28(g/mol)\\ n=2\\ X:C_2H_4\\ \to A \end{array}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
14.
A là khẳng định sai, CD không vuông góc SB
(Vì nếu \(CD\perp SB\) (1); do \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SAB\right)\Rightarrow CD\perp AB\) (vô lý do \(CD||AB\))
29 tháng 3 2022
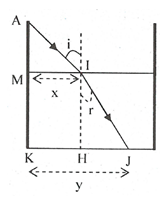
Xét \(\Delta HIJ\) vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
\(\Rightarrow\dfrac{sini}{sinr}=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{60^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow HJ=51,25cm\)
Độ dài vệt sáng:
\(y=x+HJ=85,9cm\)
Chọn B
TG
2
30 tháng 3 2022
Câu 15:
Hàm số y=ax+b, với a<>0 nghịch biến trên R khi a<0
Từ đó bạn thay vào thôi
Câu 14:
Bạn cần biến đổi về dạng y=ax+b(a<>0) rồi sau đó lần lượt thay x=0 và y=0 vào là ra
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
Các công thức lượng giác cơ bản liên quan đến góc của lớp 10:
\(sin\left(3\pi-x\right)=sin\left(2\pi+\pi-x\right)=sin\left(\pi-x\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cosx\Rightarrow sin\left(\dfrac{5\pi}{2}+x\right)=sin\left(2\pi+\dfrac{\pi}{2}+x\right)=sin\left(\dfrac{\pi}{2}+x\right)=cosx\)
\(cos\left(\dfrac{\pi}{2}+x\right)=-sinx\)
\(sin\left(\dfrac{3\pi}{2}+x\right)=sin\left(2\pi-\dfrac{\pi}{2}+x\right)=sin\left(-\dfrac{\pi}{2}+x\right)=-cosx\)
Nên pt tương đương:
\(3sin^2x-2sinx.cosx-5cos^2x=0\)
Với \(cosx=0\) không là nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow3tan^2x-2tanx-5=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{5}{3}\right)+k\pi\end{matrix}\right.\)
2
22 tháng 5 2022
`a)A` có nghĩa `<=>x-1 >= 0 <=>x >= 1`
`b)B=\sqrt{3^2 .2}+\sqrt{2^3}-\sqrt{5^2 .2}`
`<=>B=3\sqrt{2}+2\sqrt{2}-5\sqrt{2}`
`<=>B=0`
`c)` Với `a >= 0,a \ne 1` có:
`C=[a-1]/[\sqrt{a}-1]-[a\sqrt{a}-1]/[a-1]`
`C=[(a-1)(\sqrt{a}+1)-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=[a\sqrt{a}+a-\sqrt{a}-1-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=a/[a-1]`
ĐKXĐ: \(x>0\)
\(log_2\left(x^2+4\right)-log_2x-3=0\)
\(\Leftrightarrow log_2\left(x^2+4\right)=log_2x+3\)
\(\Leftrightarrow log_2\left(x^2+4\right)=log_2\left(9x\right)\)
\(\Leftrightarrow x^2+4=9x\)
\(\Leftrightarrow x^2-9x+4=0\)
\(\Rightarrow x_1+x_2=9\) theo định lý Viet