Cho tam giác ABC có góc B = 50 độ. Từ đỉnh A kẻ đường thẳng song song với BC cắt tia phân giác của góc B ở E
a) Chứng minh: Tam giác AEB là tam giác cân
b) Tính góc BAE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 12 2016
a) BE là phân giác ABC => ABE = CBE
AE //BC => AEB = CBE (so le trong)
=> ABE = AEB
=> tam giác BAE cân tại A ( đpcm)
b) Có: ABE = CBE = ABC : 2 = 50o : 2 = 25o
Tam giác BAE cân tại A có: BAE = 180o - 2.ABE
= 180o - 2.25o = 130o
21 tháng 7 2017
a) Vì BE là tia phân giác \(\widehat{B}\)
=> \(\widehat{ABE}=\widehat{CBE}\) (1)
mà AE // BC
=> \(\widehat{AEB}=\widehat{CBE}\left(soletrong\right)\) (2)
(1); (2) => \(\widehat{ABE}=\widehat{AEB}\)
=> \(\Delta AEBcân\) tại A
b) Vì BE là tia phân giác \(\widehat{B}\)
=> \(\widehat{ABE}=\widehat{AEB}=\dfrac{\widehat{ABC}}{2}=\dfrac{50^0}{2}=25^0\)
\(\Delta ABEcó:\widehat{A}+\widehat{B}+\widehat{E}=180^0\) (định lí)
hay \(\widehat{A}+25^0+25^0=180^0\)
\(\widehat{A}+50^0=180^0\)
\(\widehat{A}=180^0-50^0\)
\(\widehat{A}=130^0\)
hay \(\widehat{BAE}=130^0\)
YN
30 tháng 4 2022
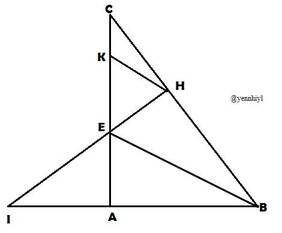
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
1 tháng 5 2022
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE
a) BE là p/g góc ABC => ABE=CBE (1)
AE//BC => AEB=CBE (so le trong) (2)
Từ (1) và (2) => ABE=AEB
=> Tam giác AEB cân tại A (đpcm)
b) Có: ABE=CBE=ABC/2=50o/2
=> 2.ABE=2.CBE=ABC=50o
Tam giác ABE cân tại A có: BAE=180o-2.ABE=180o-50o=130o
a) BE là p/g góc ABC => ABE=CBE (1)
AE//BC => AEB=CBE (so le trong) (2)
Từ (1) và (2) => ABE=AEB
=> Tam giác AEB cân tại A (đpcm)
b) Có: ABE=CBE=ABC/2=50
o/2
=> 2.ABE=2.CBE=ABC=50
o
Tam giác ABE cân tại A có: BAE=180
o-2.ABE=180
o-50
o=130
chúc bn hok tốt @_@