giải toán = cách lập pương trình:
một tam giác vuông có chu vi = 60cm và có cạnh huyền = 25cm.tính độ dài các cạnh góc vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25
độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)
Theo đề bài ta có pt :
x + (35 - x ) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0
Δ = (−35)2 − 4.1.300 = 25
x = (35+5) : 2 = 20 ; x = 35 - 20 = 15
Vậy độ dài 2 góc vuông là 20cm và 15cm
Gọi độ dài 1 cạnh góc vuông là x (cm), x < 25
độ dài cạnh góc vuông còn lại là 60 - 25 - x = 35 - x (cm)
Theo đề bài ta có pt :
x2 + (35 - x2) = 25^2 (ĐL Pytago) <=> x^2 - 35x + 300 = 0
\(\Delta=\left(-35\right)^2-4.1.300=25\)
x1 = (35+5) : 2 = 20 ; x2 = 35 - 20 = 15
Vậy độ dài 2 góc vuông là 20cm và 15cm

Gọi x là dộ dài cạnh góc vuông thứ nhất (x < 20)
=> độ dài cạnh góc vuông thứ hai : 48 - 20 -x =28 - x
Theo đề bài ta có pt:
x2 + (28 -x)2 =202 (giải pt tìm x)

Gọi độ dài đoạn thẳng ngắn hơn được chia trên cạnh huyền là x (cm) với x>0
\(\Rightarrow\) Độ dài đoạn còn lại là \(x+14\)
Áp dụng hệ thức lượng trong tam giác vuông:
\(24^2=x\left(x+14\right)\)
\(\Leftrightarrow x^2+14x-576=0\Rightarrow\left[{}\begin{matrix}x=18\\x=-32\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\) Độ dài cạnh huyền là: \(18+\left(18+14\right)=50\left(cm\right)\)
Diện tích tam giác: \(S=\dfrac{1}{2}.24.50=600\left(cm^2\right)\)

Gọi độ dài các cạnh góc vuông của tam giác lần lượt là 5k và 12k với k> 0. Dùng định lý Py-ta-go tính được độ dài cạnh huyền là 13k, do đó
5k +12k + 13k = 30 => k = 1.
Từ đó độ dài cạnh huyền là 13 cm.

Gọi b, c là độ dài các cạnh góc vuông, a là độ dài cạnh huyền (tính bằng cm) ( 0 < b; c < a)
+) Do các cạnh góc vuông tỉ lệ với 7 và 24 nên:
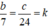 ⇒ b = 7k, c = 24k.
⇒ b = 7k, c = 24k.
Theo định lý Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
Nên a = 25k.
Theo đề bài, chu vi tam giác bằng 112 cm nên: a + b + c = 112 (cm).
Suy ra: 25k + 7k + 24k = 112
Hay 56k = 112
Từ đó ta tính được k = 2. Vậy a = 50cm.

Lời giải:
Gọi độ dài cạnh góc vuông lần lượt là $a$ và $b$ ($a>b>0$) (cm)
Áp dụng định lý Pitago: $a^2+b^2=60^2=3600(*)$
$a-b=12$
$\Leftrightarrow a=b+12$. Thay vào $(*)$ thì:
$(b+12)^2+b^2=3600$
$\Leftrightarrow 2b^2+24b-3456=0$
$\Leftrightarrow b^2+12b-1728=0$
$\Leftrightarrow (b-36)(b+48)=0$
Do $b>0$ nên $b=36$ (cm)
$a=b+12=36+12=48$ (cm)