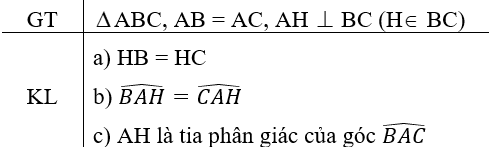
cho tam giác ABC cân tại a ( góc a= 90 độ ) dựng AH vuông góc với BC tại H ( H thuộc BC)
a chứng minh tam giác ABC = tam giác AHC và HB=HC
b với AB =30cm bc =36cm tính độ dài AH
c kẽ đường trung tuyến BM của tam giác ABC cắt AH tại G tính độ dài AG và BM
gấp ạ giúp mình câu c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KB
9 tháng 5 2021
a) Chứng minh HB=HC: Xét ΔAHB và ΔAHC có: ∠AHB=∠AHC=90(độ) AH cạnh chung AB=AC(gt) ⇒ ΔAHB = ΔAHC (ch-cgv) ⇒ HB=HC (2 cạnh tương ứng)
b) Ta có: HB=HC=BC/2=6/2=3(cm) Ta có: ΔAHB vuông tại H. ⇒ AH(mũ 2)+BH(mũ 2)=AB(mũ 2) ⇒ AH(mũ 2)=AB(mũ 2)-BH(mũ 2) =4(mũ 2)-3(mũ 2)=16-9=7 ⇒ AH=√7(cm)
c) Ta có: ΔAHB = ΔAHC ⇒ ∠BAH=∠CAH Xét ΔAHD và ΔAHE có: ∠D=∠E=90(độ) AH cạnh chung ∠BAH=∠CAH (gt) ⇒ ΔAHD = ΔAHE (ch-gn) ⇒ DH=EH ⇒ ΔHDE cân tại H.
29 tháng 4 2018
Hỏa Long Natsu bác eii, cái bài này là ae mk tự vẽ hình hay sao ý.
a) Xét \(\Delta AHB\text{ và }\Delta AHC\)
\(AB=AC\)
\(\widehat{A_1}=\widehat{A_2}\)
AH là cạnh chung
Nên: \(\Delta AHB=\Delta AHC\left(c-g-c\right)\)
\(\Rightarrow BH=CH\left(2\text{ cạnh tương ứng}\right)\)
\(\Rightarrow\Delta ABC\perp AH\left(\text{là phân giác cũng vừa là đường cao}\right)\)
\(\Rightarrow AH\perp BC\)
b) \(BH=\frac{36}{2}=18\left(cm\right)\)
\(AB^2=AH^2+BH^2\left(\text{áp dụng định lý Py-Ta-Go}\right)\)
\(AH^2=AB^2-BH^2\)
\(AH^2=30^2-18^2\)
\(AH^2=576\)
\(\Rightarrow AH=\sqrt{576}=24\left(cm\right)\)
c) \(AG=\frac{2}{3}.AH\)
\(\Rightarrow AH.\frac{2}{3}=24.\frac{2}{3}=16\left(cm\right)\)
\(AM=\frac{AB}{2}=\frac{30}{2}=15\left(cm\right)\)
\(\Rightarrow BA^2=AM^2+BM^2\)
\(\Rightarrow MB^2=BA^2-BM^2\)
\(MB^2=30^2-15^2\)
\(MB^2=\sqrt{675}=26\)
d) Bạn tự giải nha
20 tháng 8 2016
a) Vì AH là đường trung tuyến của tam giác ABC cân tại A:
nên HB=HC
Xét tam giác AHB và tam giác AHC:
có:+AB=AC( tam giác ABC cân tại A)
+HB=HC(cmt)
+AH: cạnh chung
Vậy tam giác AHB=tam giác AHC(c.c.c)
b) Vì tam giác AHB=tam giác AHC(cmt)
nên: góc AHB=góc AHC=90 độ( 2 góc tương ứng )
c) \(HB=HC=\frac{BC}{2}=\frac{10}{2}=5cm\)
Áp dụng định lí Pytago vào tam giác ABH vuông tại H:
có: \(AB^2=AH^2+BI^2\)
hay:\(13^2=AH^2+5^2\)
\(\Rightarrow AH^2=13^2-5^2\)
\(\Leftrightarrow AH=\sqrt{13^2-5^2}=12\)
Vậy AH=12cm
BD
20 tháng 8 2016
a)
theo giả thiết ta có :
AH là đường trung tuyến \(\Rightarrow BH=HC\)
xét \(\Delta AHB\) và \(\Delta AHC\) có:
\(AB=AC\) (gt)
\(AH\) chung
\(BH=HC\) ( cmt)
\(\Rightarrow\Delta AHB=\Delta AHC\) (c.c.c)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\) (2 góc tương ứng )
b)
ta có : \(\widehat{AHB}+\widehat{AHC}=180^0\) ( kề bù )
mà \(\widehat{AHB}=\widehat{AHC}\) (theo a)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=\frac{180^0}{2}=90^0\)
c) \(BH=HC=\frac{10}{2}=5\) (cm)
xét \(\Delta AHB\perp\) tại H
áp dụng định lý py-ta-go ta có:
\(AB^2=AH^2+BH^2\)
\(13^2=AH^2+5^2\)
\(\Rightarrow AH^2=169-25=144=\sqrt{144}=12\) (cm)
11 tháng 4 2018
ban tu ve hinh nha
a) Xet tam giac ahb ca tam giac ahc co
ab=ac(tam giac abc can tai a)
ah chung
hb=hc(t\c duong trung tuyen trong tam giac)
\(\Rightarrow\)tam giac ahb=tam giac ahc(c-c-c)
b) vi tam giac ahb=tam giac ahc nen
goc ahb=ahc(2 goc t\u) ma 2 goc nay ke bu nen ahb=ahc=1\2.180=90 do
c) ap dung dinh ly pi ta go trong tam giac ahb(goc h=90 do) co
ah^2=ab^2-hb^2
ah^2=13^2-(10\2)^2
ah^2=13^2-5^2
ah^2=169-25
ah^2=144
ah=\(\sqrt{144}\)
ah=12
k dum mk nha
25 tháng 6 2023
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC
b: BH=CH=6/2=3cm
AH=căn 5^2-3^2=4cm
c: Xét ΔABC có
AH là trung tuyến
G là trọng tâm
=>A,G,H thẳng hàng
d: Xét ΔABG và ΔACG có
AB=AC
góc BAG=góc CAG
AG chung
=>ΔABG=ΔACG
=>góc ABG=góc ACG
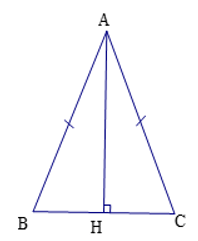
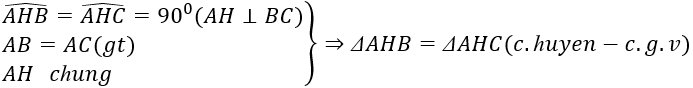
a: XétΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=BC/2=18(cm)
nên AH=24(cm)