Câu 7,8,9 ạ. Cảm ơn mọi người nhiều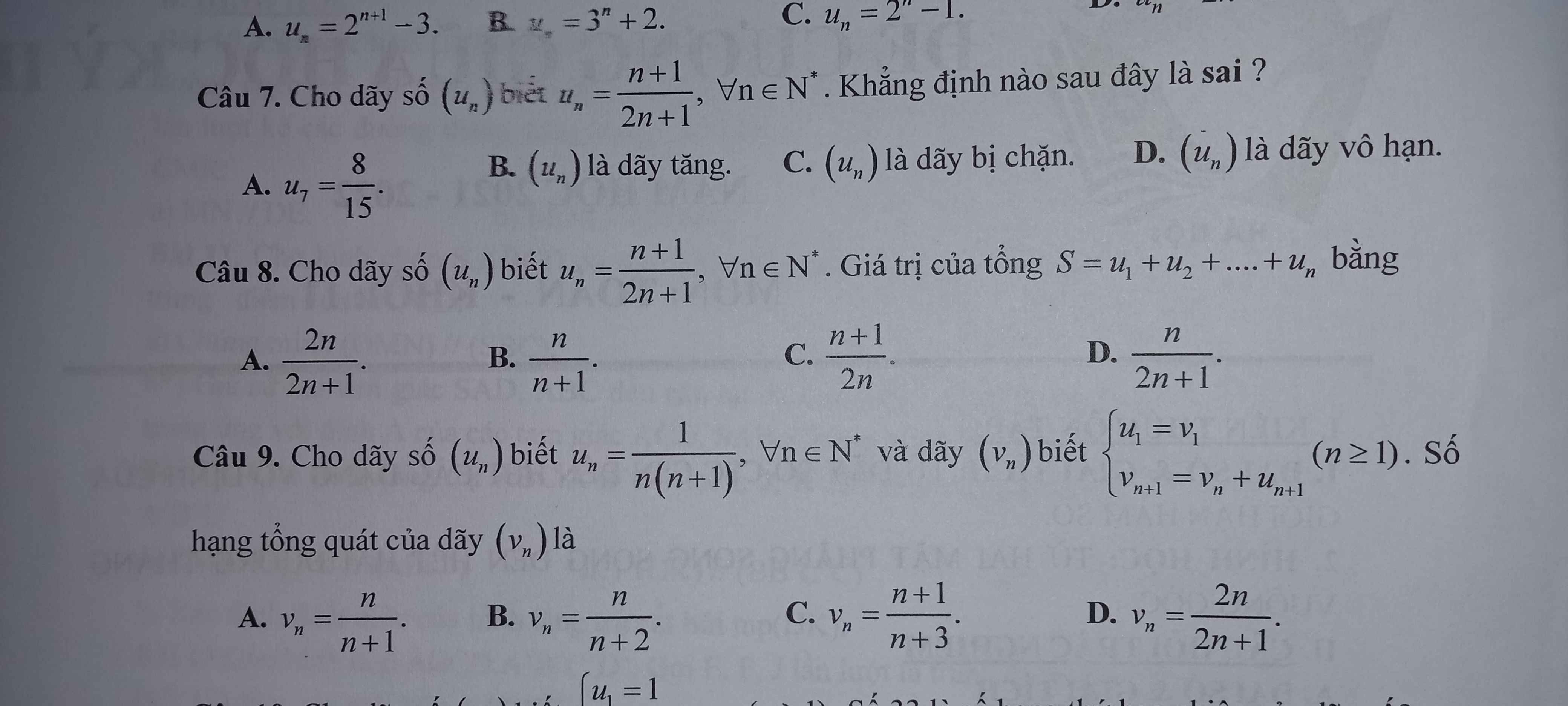 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
XT
3
NA
2
Y
17 tháng 1 2023
\(c,\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-2}+\dfrac{2}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{y+1}+\dfrac{3}{y+1}=5\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{y+1}=5\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+1=1\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=0\left(2\right)\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\left(1\right)\end{matrix}\right.\)
Thay \(\left(2\right)\) vào \(\left(1\right)\) :
\(\dfrac{4}{x-2}-\dfrac{3}{0+1}=1\)
\(\Rightarrow\dfrac{4}{x-2}-3=1\)
\(\Rightarrow\dfrac{4}{x-2}=4\)
\(\Rightarrow x-2=1\)
\(\Rightarrow x=3\)
Vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(3;0\right)\)
17 tháng 1 2023
c: =>4/x-2+2/y+1=6 và 4/x-2-3/y+1=1
=>5/y+1=5 và 2/x-2+1/y+1=3
=>y+1=1 và 2/x-2+1=3
=>y=0 và x-2=1
=>x=3 và y=0
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
27.
Gọi 3 cạnh của tam giác lần lượt là a;b;c với c là cạnh huyền
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=3\\a+c=2b\\a^2+b^2=c^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=3\\3-b=2b\\a^2+b^2=c^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=2-c\\b=1\\\left(2-c\right)^2+1=c^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{4}\\b=1\\c=\dfrac{5}{4}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
28.
Cấp số cộng thứ nhất có \(u_1=4;d=3\Rightarrow u_n=4+3\left(n-1\right)=3n+1\)
Cấp số cộng thứ hai có \(u_1=1;d=5\Rightarrow u_m=1+5\left(m-1\right)=5m-4\)
Trong đó \(1\le m;n\le100\) (do mỗi CSC có 100 số hạng)
Số có mặt trong cả 2 CSC thỏa mãn:
\(3n+1=5m-4\)
\(\Leftrightarrow3n=5\left(m-1\right)\)
\(\Rightarrow n⋮5\Rightarrow n=5k\)
\(\Rightarrow1\le5k\le100\Rightarrow1\le k\le20\)
\(\Rightarrow\) Có 20 giá trị k hay có 20 số thỏa mãn
TA
1
18 tháng 10 2020
Gọi 3 số nguyêntố đó là: a, b, c
Ta có: 5(a+b+c)
=>abc chia hết cho 5, do a,b,c nguyên tố
=>chỉ có trường hợp 1 trong 3 số bằng 5, giả sử a=5
=>bc=b+c+5=>(b-1)(c-1)=6
trương hợp 1: b - 1 = 1=>b=2;c - 1 = 6=>c=7
trường hợp 2: b - 1= 2, c - 1 = 3 =>c=4(loại)
vậy 3 số nguyên tố đó là: 2;5;7
NP
0
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
7.
\(u_1=\dfrac{1+1}{2.1+1}=\dfrac{2}{3}\) ; \(u_2=\dfrac{2+1}{2.2+1}=\dfrac{3}{5}\Rightarrow u_1-u_2=\dfrac{2}{3}-\dfrac{3}{5}=\dfrac{1}{15}>0\)
\(\Rightarrow\) Dãy đã cho là dãy giảm nên đáp án B sai
8.
Đề bài sai, rõ ràng \(u_1+u_2>1\) nhưng tất cả công thức trong dãy đều cho tổng nhỏ hơn 1
9.
\(u_{n+1}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}\); \(v_1=u_1=\dfrac{1}{2}\)
\(v_{n+1}=v_n+\dfrac{1}{\left(n+1\right)\left(n+2\right)}=v_n+\dfrac{1}{n+1}-\dfrac{1}{n+2}\)
\(\Rightarrow v_{n+1}+\dfrac{1}{\left(n+1\right)+1}=v_n+\dfrac{1}{n+1}\)
Đặt \(v_n+\dfrac{1}{n+1}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=v_1+\dfrac{1}{2}=1\\x_{n+1}=x_n=...=x_1=1\end{matrix}\right.\)
\(\Rightarrow v_n+\dfrac{1}{n+1}=1\Rightarrow v_n=1-\dfrac{1}{n+1}=\dfrac{n}{n+1}\)