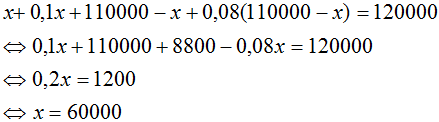Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu động , kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai . Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 3 2018
Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y
(x, y > 0, triệu đồng; x < 2,17, y < 2,17)
Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x
+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.
Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)
Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x
+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.
Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:
1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)
Từ (1) và (2) ta có hệ phương trình :
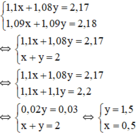
Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
CM
26 tháng 5 2017
Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y
(x, y > 0, triệu đồng; x < 2,17, y < 2,17)
Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x
+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.
Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)
Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x
+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.
Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:
1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)
Từ (1) và (2) ta có hệ phương trình :
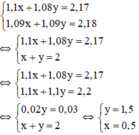
Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .
4 tháng 4 2017
Giả sử không kể thuế VAT, người đó phải trả x triệu đồng cho loại hàng thứ nhất, y triệu đồng cho loại hàng thứ hai. Khi đó số tiền phải trả cho loại hàng thứ nhất, (kể cả thuế VAT 10%) là triệu đồng, cho loại hàng thứ hai, với thuế VAT 8% là
triệu đồng. Ta có phương trình
+
= 2,17 hay 1,1x + 1,08y = 2,17
Khi thuế VAT là 9% cho cả hai loại hàng thì số tiền phải trả là: = 2,18
hay 1,09x + 1,09y = 2,18.
Ta có hệ phương trình:
Giải ra ta được: x = 0,5; y = 1,5
Vậy loại thứ nhất 0,5 triệu đồng, loại thứ hai 1,5 triều đồng.
25 tháng 5 2017
Ai giải thích hộ em tại sao chỗ kia lại là và
được không ạ ? Em không hiểu lắm
30 tháng 1 2021
Gọi x(triệu đồng) là số tiền người đó phải trả khi mua loại hàng thứ 1, y(triệu đồng) là số tiền người đó phải trả khi mùa loại hàng thứ 2(Điều kiện: \(\left\{{}\begin{matrix}x\in Z^+\\y\in Z^+\end{matrix}\right.\))
Số tiền phải trả cho loại hàng thứ nhất kể cả thuế VAT 10% là: \(\dfrac{11}{10}x\)(triệu đồng)
Số tiền phải trả cho loại hàng thứ hai kể cả thuế VAT 8% là: \(\dfrac{27}{25}y\)(triệu đồng)
Vì khi mua hai loại hàng thì người đó phải trả tổng cộng 2,17 triệu đồng kể cả thuế VAT đối với 10% thuế VAT của loại hàng thứ nhất và 8% thuế VAT của loại hàng thứ hai nên ta có phương trình:
\(\dfrac{11}{10}x+\dfrac{27}{25}y=\dfrac{217}{100}\)
Số tiền phải trả cho mặt hàng thứ nhất kể cả thuế VAT 9% là:
\(\dfrac{109}{100}x\)(triệu đồng)
Số tiền phải trả cho mặt hàng thứ hai kể cả thuế VAT 9% là:
\(\dfrac{109}{100}y\)(triệu đồng)
Vì khi thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng nên ta có phương trình:
\(\dfrac{109}{100}x+\dfrac{109}{100}y=\dfrac{218}{100}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{11}{10}x+\dfrac{27}{25}y=\dfrac{217}{100}\\\dfrac{109}{100}x+\dfrac{109}{100}y=\dfrac{218}{100}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0.5\\y=1.5\end{matrix}\right.\)
Vậy: số tiền người đó phải trả cho loại thứ nhất là 500 nghìn đồng, loại thứ hai là 1,5 triều đồng.
CM
18 tháng 1 2018
* Phân tích:
Vì trong 120000 Lan trả có 10000 thuế VAT nên giá gốc của hai sản phẩm không tính VAT là 110000 đồng.
| Giá gốc | Thuế VAT | |
| Hàng thứ 1 | x | 0,1.x |
| Hàng thứ 2 | 110000 – x | 0,08.(110000 – x) |
Thuế VAT của cả hai mặt hàng là 10 nghìn nên có phương trình:
0,1x + 0,08(110000 – x) = 10000.
* Giải
Gọi giá gốc của mặt hàng thứ nhất là x (0 < x < 110000 đồng).
Vì trong 120000 đồng Lan trả đã có 10000 đồng thuế VAT nên tổng giá gốc của cả hai mặt hàng chỉ bằng: 120000 – 10000 = 110000 (nghìn đồng).
⇒ Giá gốc của mặt hàng thứ hai là: 110000 – x ( đồng).
Thuế VAT của mặt hàng thứ nhất bằng: 10%.x = 0,1x (đồng).
Thuế VAT của mặt hàng thứ hai bằng: 8%.(110000 – x) = 0,08.(110000 – x) (đồng).
Thuế VAT của cả hai mặt hàng bằng: 0,1x + 0,08(110000 – x) (nghìn đồng).
Theo đề bài, tổng thuế VAT của cả hai mặt hàng là 10000 đồng nên ta có phương trình:
0,1x + 0,08(110000 – x) = 10000
⇔ 0,1x + 8800 – 0,08x = 10000
⇔ 0,02x = 1200
⇔ x = 60000 (thỏa mãn điều kiện).
Vậy không kể VAT thì giá của mặt hàng thứ nhất là 60000 đồng, giá của mặt hàng thứ hai là 110000 – 60000 = 50000 đồng.
1 tháng 8 2017
Số tiền mà Lan phải trả không kể VAT là:
120-10=110 (nghìn đồng)
Gọi x (nghìn đồng) là số tiền (không VAT) Lan phải trả cho loại hàng I
\Rightarrow Số tiền ( không VAT)Lan phải trả cho loại hàng II là 110-x (nghìn đồng)
\Rightarrow Thuế VAT phải trả cho loại hàng I là: x.10% (nghìn đồng)
Thuế VAT phải trả cho loại hàng II là: (110-x).8% (nghìn đồng)
Do tổng thuế VAT là 10 nghìn đồng
\Rightarrow Ta có phương trình:
x.10% + (110-x).8% = 10
\Leftrightarrow x10x10 + 8,8 - 2x252x25 = 10
\Leftrightarrow 5x−4x505x−4x50 = 1,2
\Leftrightarrow x=60
\Rightarrow 110-x =50
Vậy, nếu không kể VAT thì Lan phải trả loại hàng I 60000 và loại hàng II 50000
LH
22 tháng 4 2017
Số tiền thật sự Lan đã trả cho hai loại hàng là:
120000 - 10% 120000 = 110000 (đồng)
Gọi x (đồng) là tiền mua loại hàng thứ nhất không kể thuế VAT (0 < x < 110000)
Tiền mua loại hàng thứ hai không kể thuế VAT: 110000 – x
Số tiền thật sự Lan đã trả cho loại hàng 1: x + 0,1x
Số tiền thật sự Lan đã trả cho loại hàng 2: 110000 – x + 0,08(110000 – x)
Ta có phương trình:
x = 60000 thỏa điều kiện.
Vậy số tiền trả cho loại hàng thứ nhất là 60000 đồng (không kể thuế VAT).
Số tiền phải trả cho loại hàng thứ hai không kể thuế VAT là:
110000 - 60000 = 50000 đồng.
4 tháng 3 2018
Số tiền Lan đã trả cho 2 loại hàng (không gồm VAT):
120000 - 10000 = 100000 (đ)
Gọi số tiền cần trả cho loại hàng thứ nhất là a, loại hàng thứ 2 là b (đơn vị: nghìn đồng)
Ta có:
10%a + 8%b = 10 (1)
a + b = 110
\(\Rightarrow\) a = 110 - b (2)
Thế (2) vào (1), ta có:
10%(110 - b) + 8%b = 10
\(\Leftrightarrow\) 10% . 110 - 10%b + 8%b = 10
\(\Leftrightarrow\)11 - 2%b = 10
\(\Leftrightarrow\) 11 - 10 = 2%b
\(\Leftrightarrow\) 2%b = 1
\(\Leftrightarrow\) b = 50 (nghìn đồng)
\(\Rightarrow\) a = 110 - 50 = 60 (nghìn đồng)
Vậy giá tiền hai loại hàng lần lượt là 60000đ và 50000đ.
0
5 tháng 4 2018
Gọi x (đồng) là tiền mua loại hàng thứ nhất không kể thuế VAT (0 < x < 110000)
Tiền mua loại hàng thứ hai không kể thuế VAT: 110000 - x
Số tiền thất sự Lan đã trả cho loại hàng 1: x + 0,1x
Số tiền thất sự Lan đã trả cho loại hàng 2:
110000 - x + 0,08(110000 - x)
Ta có phương trình
x+ 0,1x + 110000 - x + 0,08(110000 - x) = 120000
⇔ 0,1x + 110000 + 8800 - 0,08x = 120000
⇔ 0,02x = 1200
⇔ x = 60000
x = 6000 thoả mãn điều kiện
Vậy số tiền trả cho loại hàng thứ nhất là 60000 đồng (không kể thuế VAT)
Số tiền phải trả cho loại hàng thứ hai không kể thuế VAT: 50000 đồng
5 tháng 4 2018
Gọi x (đồng) là tiền mua loại hàng thứ nhất không kể thuế VAT (0 < x < 110000)
Tiền mua loại hàng thứ hai không kể thuế VAT: 110000 - x
Số tiền thất sự Lan đã trả cho loại hàng 1: x + 0,1x
Số tiền thất sự Lan đã trả cho loại hàng 2:
110000 - x + 0,08(110000 - x)
Ta có phương trình
x+ 0,1x + 110000 - x + 0,08(110000 - x) = 120000
⇔ 0,1x + 110000 + 8800 - 0,08x = 120000
⇔ 0,02x = 1200
⇔ x = 60000
x = 6000 thoả mãn điều kiện
Vậy số tiền trả cho loại hàng thứ nhất là 60000 đồng (không kể thuế VAT)
Số tiền phải trả cho loại hàng thứ hai không kể thuế VAT: 50000 đồng
