Cho tam giác ABC nhọn các đường cao BI , CK , điểm M thuộc cạnh BC , gọi D, E
lần lượt là hình chiếu của M trên AB , AC . Gọi D’ là hình chiếu của D trên AC , E’ là hình
chiếu của E trên AB , H là giao điểm của DD’ và EE’ . CMR : K , H , I thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SV
22 tháng 4 2015
Tam giác vuông ADH và tam giác vuông AHB có góc A chung nên đồng dạng => AD/AH = AH/AB => AH2 = AD.AB
cmtt ta cũng có AH2 = AE.AB => AD.AB = AE. AC
Xét tam giác ABE và tam giác ACD có góc A chung và AB/AC = AE/AD (cmt)
=> tg ABE đồng dạng tg ACD (c-g-c) => góc ABE = góc ACD
đến đây bn tự cm tiếp nhé!
10 tháng 5 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hình chữ nhật
b: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
góc DAH chung
=>ΔADH đồng dạng với ΔAHB
c: ΔAHC vuông tại H có HE vuông góc AC
nên HE^2=AE*EC
KT
21 tháng 12 2017
a) \(\Delta ABC\) có MA = MB; NA = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)MN // BC
\(\Rightarrow\)Tứ giác BMNC là hình thang
b) \(\Delta ABC\)có NA = NC; QB = QC
\(\Rightarrow\)NQ // AB; NQ = 1/2 AB
mà MA = 1/2 AB
\(\Rightarrow\)NQ = MA
Tứ giác AMQN có NQ // AM; NQ = AM
\(\Rightarrow\)AMQN là hình bình hành
9 tháng 5 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
=>ΔABH đồng dạngvói ΔAHD
c: ΔHAC vuông tại H có HE là đường cao
nên HE^2=AE*EC
1 tháng 7 2023
a: Xét ΔABD có
AI vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
góc HAI=góc KAI
=>ΔAHI=ΔAKI
=>HI=KI
c: HI=KI
KI<ID
=>HI<ID
14 tháng 4 2022
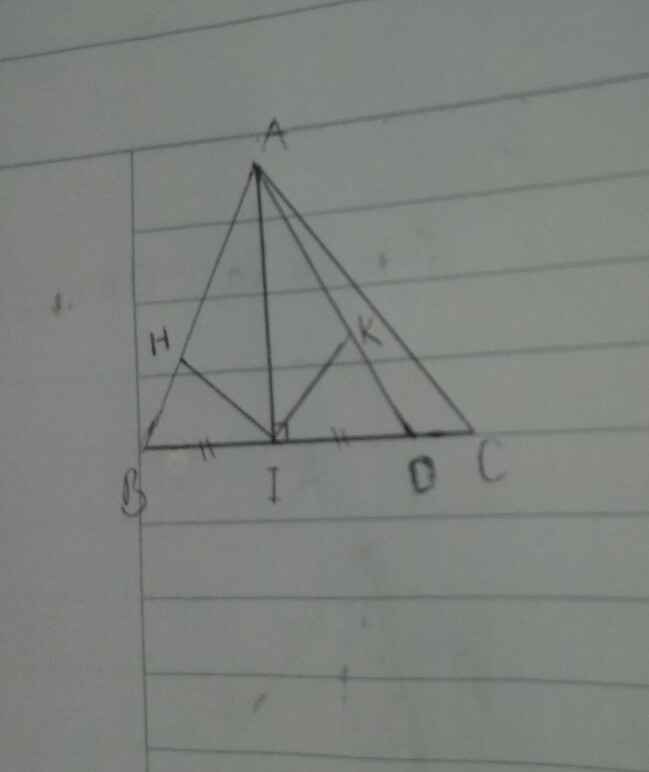
rồi từ câu a) là sai đề nhaaaa em ( ko thể chứng minh đc - do AB < AC < BC)
