Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tam giác ABC cân
=> góc ABC=góc ACB
góc MBA+góc ABC=180độ (kề bù)
góc NCA+góc ACB=180độ(kề bù)
=> góc ABM=góc ACN
xét 2 tam giác ABM và ACN có:
AB=AC(tam giác ABC cân )
góc ABM=góc ACN(chứng minh trên)
BM=CN(gt)
=> 2 tam giác ABM=ACN(c.g.c)
=> AM=AN(2 cạnh tương ứng)
=> tam giác AMN cân ở A
b) tam giác AMN cân ở A
=> góc M=góc N
xét 2 tam giác MHB và NKC có:
góc MHB=góc NKC(=90độ)
MB=NC(gt)
góc M =góc N(chứng minh trên)
=> 2 tam giác MHB=NKC(cạnh huyền - góc nhọn)
=> BH=CK(2 cạnh tương ứng)
c) ta có : AM=AN (theo a)
HM=KN (tam giác MHB=tam giác NKC)
AM = AH+HM
AN= AK+ KN
=> AH= AK
d) tam giác MHB=tam giác NKC(theo b)
=> góc HBM=góc KCN(2 góc tương ứng)
góc HBM=góc OBC(đối đỉnh)
góc KCN=góc OCB(đối đỉnh)
=> góc OBC=góc OCB
=> tam giác OBC cân ở O
e) tam giác ABC có AB=AC ; góc BAC=60độ
=> tam giác ABC đều
=> AB=AC=BC
mà BC=BM(gt)
=> BM=AB
=>tam giác ABM cân ở B
góc ABC + góc ABM=180độ (kề bù)
=> góc ABM =180độ - góc ABC
=180độ-60độ
=120độ
tam giác ABC cân ở B
=> góc BAM=góc BMA =(180độ-góc ABM) / 2=1800−12002=6002=3001800−12002=6002=300
vậy góc AMN=30độ

Vẽ hình:
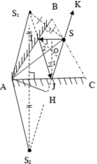
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.
mấy dòng cúi đọc chả hiểu j nhưng mình vẫn chép
thank you so much
I LOVE YOU chụt chụt...

a) Ta áp dụng định lí Py-ta -go cho tam giác ABC vuông tại B là:
AB2 + BC2 = AC2
52 +122 =AC2
169=AC2
√169=AC
15 =AC
VẬY: AC= 15 cm
b) Xét △ABE và △DBE có:
góc DBE = góc ABE = 90( GT)
DB=AB(gt)
BE chung
➩ △ABE = △DBE (cạnh huyền - cạnh góc vuông)
➩ DE=AE (2 cạnh tương ứng bằng nhau)
➩ △EAD cân tại E (đpcm)

a) xét tam giác ABE và tam giác AFE
có BAE=EAF
BEA=FEA
AE chung
=> hai tam iác bằng nhau
b)HF=DK
HK_ chung
FHK=HKB (so le trong)
=> hai tam giác bằng nhau
xin lỗi nha nhưng câu c mình chịu ![]()
chúc bạn hok tốt!!!!!!!!!!!!

Từ I hạ IG; IK lần lượt vuông góc với AC; AB
Do BI; CI là phân giác góc và C nên IH=IG=IK
=> HC=GC=3 (cm) ; HB=KB=2 (cm)
Dễ dàng chứng minh 2 tam giác AKI và AGI là 2 tam giác vuông cân
=> IG=AG; IK=AK. Mà IH=IK=IG => AG=AK=IH=1 (cm)
=> CABC= AK+KB+HB+HC+AG+GC=1+2+2+3+1+3=12 (cm).


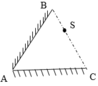

rồi từ câu a) là sai đề nhaaaa em ( ko thể chứng minh đc - do AB < AC < BC)
cô em cho vậy mà chị