cho tam giác ABC có AM là trung tuyến vừa là phân giác của góc BAC. CMR tam giác ABC cân tại A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
10 tháng 4 2016
Xét tam giác AMB và tam giác AMC có:
Góc BAM=Góc CAM(AM là đường phân giác góc BAC)
Chung AM
BM=CM(AM là đường trung tuyến góc BAC)
=>Tam giác AMB=Tam giác AMC.
=>AB=AC.
=>Tam giác ABC cân tại A(ĐPCM).
10 tháng 4 2016
mk có cách khác:
vẽ MH vuông góc AB ; MK vuông góc AC
vì AM là trung tuyến vừa là p/giác của góc BAC
=> MH = MK
xét tam giác MHB và tam giác MKC có:
góc H = góc K = 900 cách vẽ)
MH = MK (cmt)
BM = CM (gt)
=> tam giác MHB = tam giác MKC ( ch-gn)
=> góc B = góc C
=> tam giác ABC cân tại A
AH
Akai Haruma
Giáo viên
12 tháng 6 2021
Lời giải:
a) Sửa lại thành $\triangle ABM=\triangle ACM$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (do $ABC$ là tam giác cân tại $A$)
$\widehat{ABM}=\widehat{ACM}$ (do $ABC$ là tam giác cân tại $A$)
$AM$ chung
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b) Từ tam giác bằng nhau trên suy ra:
$\widehat{BAM}=\widehat{CAM}$ nên $AM$ là phân giác $\widehat{BAC}$
18 tháng 4 2023
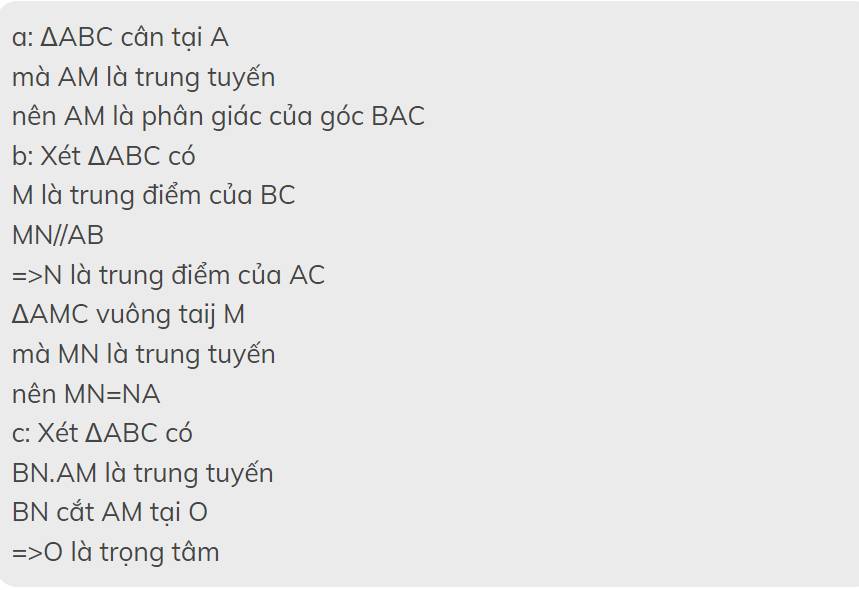
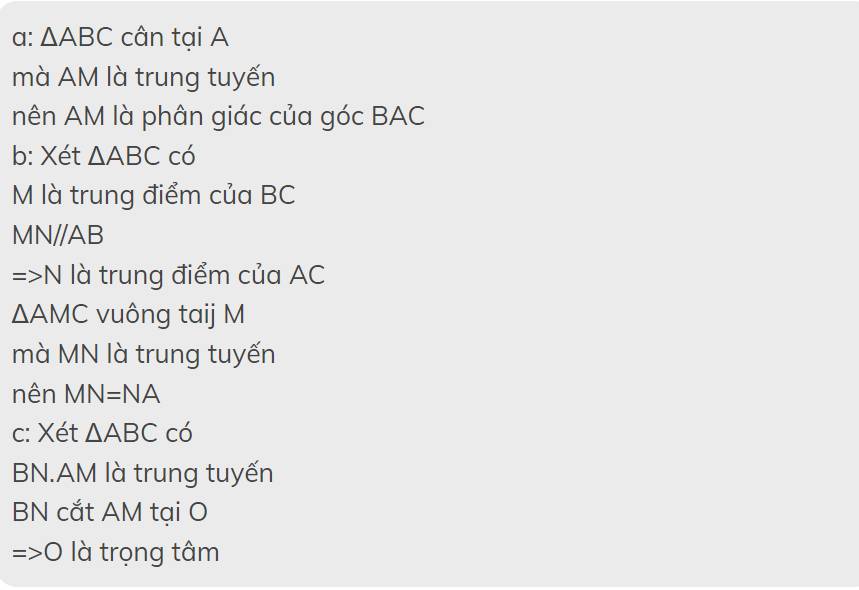
a: ΔABC cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
b: Xét ΔABC có
M là trung điểm của BC
MN//AB
=>N là trung điểm của AC
ΔAMC vuông taij M
mà MN là trung tuyến
nên MN=NA
c: Xét ΔABC có
BN.AM là trung tuyến
BN cắt AM tại O
=>O là trọng tâm
