cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chưa nửa đường tròn vẽ tiếp tuyến Ax và By . Điểm M thuộc (O) sao cho tiếp tuyến tại M cắt Ax, By lần lượt tại C, D.a) Cm: CD= AC+BDb) Cm: OC vuông AMc) Gọi E là giao điểm AM và Oc, F là giao điểmcủa BM và OD . Tứ giác MÈO là hình gì? Tại...
Đọc tiếp
cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chưa nửa đường tròn vẽ tiếp tuyến Ax và By . Điểm M thuộc (O) sao cho tiếp tuyến tại M cắt Ax, By lần lượt tại C, D.
a) Cm: CD= AC+BD
b) Cm: OC vuông AM
c) Gọi E là giao điểm AM và Oc, F là giao điểmcủa BM và OD . Tứ giác MÈO là hình gì? Tại sao?
.
. Tính MA và MB.
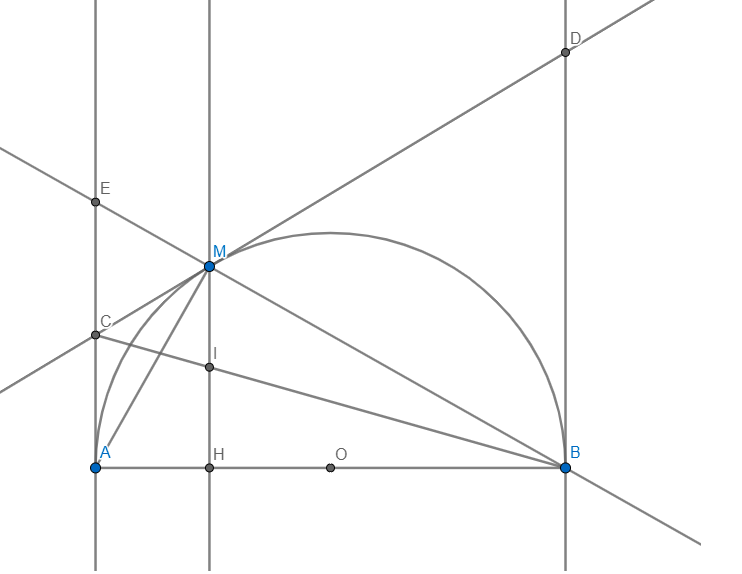
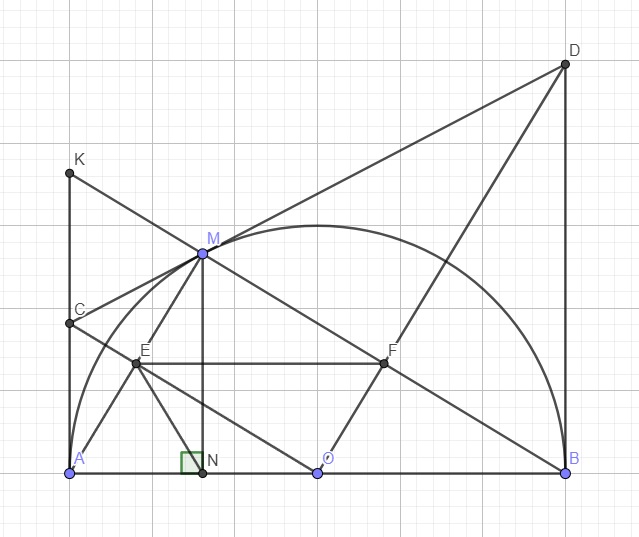
a) Nối B với M
Xét tam giác OBM,có:
OB=OM(Cùng là bán kính)
=>Tam giác OBM cân tại O
=>Góc OMB=Góc OBM (2gocs tương ứng)
Ta có:By tiếp tuyến với đg tròn (O) tại B
=>Góc OBy=90o(t/c...)
Hay góc OBC=90o (C∈By)
CD tiếp tuyến với đg tròn (O)
=>Góc OMD=góc OMC=90o(t/c...)
Ta có:OBM+MBD=OBD
OMB+BMD=OMD
MàOBM=OMB (cmt)
OBD=OMD (=90o)
=>MBD=BMD
Xét tam giác BMD, có:
MBD=BMD (cmt)
=>Tam giác BMD cân tại D
=>BD=MD (2 cạnh tương ứng)
Nối A với M
Xét tam giác AOM,có:
OA=OM (cùng là R)
=>TAm giác OAM cân tại O
=>OAM=OMA(2 góc tương ứng)
Ta có :Ax tiếp tuyến với đg tròn (O) tại A
=>OAx=90o
HayOAC=90o (C∈Ax)
Ta có :OAM+MAC=OAC
OMA+AMC=OMC
Mà:OAM=OMA(cmt)
OAC=OMC(=90o)
=>MAC=AMC
Xét tam giác ACM,có:
MAC=AMC(cmt)
=>Tam giác ACM cân tại C
=>AC=CM(2 cạnh tương ứng)
Ta có:CM+MD=CD
Mà:CM=AC(cmt)
MD=BD(cmt)
=>AC+BD=CD
b)Gọi E là gđ của AM và CO
Ta có : AC cắt CM tại C
Mà AC và CM là tiếp tuyến của đg tròn (O)
=>AC=MC;CO là p/g của ACM(...)
Vì CO là p/g của ACM(cmt)
=>ACO=MCO
Hay ACI=MCI
Xét tam giác ACI và tam giác MCI,có:
AC=MC(cmt)
ACO=MCO(cmt)
CI là cạnh chung
=>Tam giác ACI=Tam giác MCI(c.g.c)
=>AIC=MIC(2 góc tương ứng);AI=MI
Ta có:AIC+MIC=180o(2 góc bù nhau)
Mà AIC=MIC(cmt)
=>AIC=90o
=>OC⊥AM tại I