Cho đường tròn (O) đường kính AB. Trên cùng nửa đường tròn lấy hai điểm C, D. Kẻ CH vuông góc với AB tại H, CH cắt (O) tại điểm thứ hai E. Kẻ AK vuông góc với CD tại K, AK cắt (O) tại điểm thứ hai F. Chứng minh:
a, Hai cung nhỏ C F ⏜ và D B ⏜ bằng nhau
b, Hai cung nhỏ
B
F
⏜
và
D
E
⏜
bằng nhau
c, DE = BF

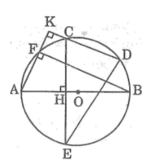

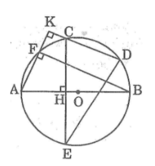
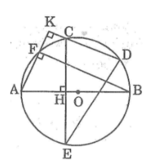
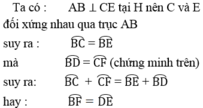

a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây