Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Mặt bên ABB’A’ có diện tích bằng a 2 3 . Gọi M; N lần lượt là trung điểm của A’B; A’C . Tính tỉ số thể tích của hai khối chóp A’. AMN và A’.ABC.
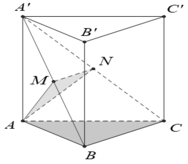
A. 1 2
B. 1 3
C. 1 4
D. 1 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
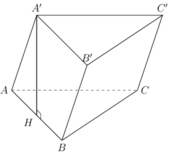
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8

a) Với hình lăng trụ đứng ABC.ABC, diện tích tứ giác ABBA bằng 2a^2 và đáy ABC là tam giác vuông cân tại A, ABa. Thể tích khối lăng trụ ABC.ABC có thể tính bằng công thức: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Vì đáy ABC là tam giác vuông cân nên diện tích đáy là \(\frac{1}{2} \times a \times a = \frac{1}{2}a^2\). Chiều cao của lăng trụ chính là cạnh AB, vì tam giác ABa là tam giác vuông cân nên \(AB = \sqrt{2}a\). Do đó, thể tích khối lăng trụ ABC.ABC là: \(V = \frac{1}{3} \times \frac{1}{2}a^2 \times \sqrt{2}a = \frac{\sqrt{2}}{6}a^3\). b) Với hình lăng trụ đứng ABC.ABC, góc giữa (ABC) và (ABC) bằng 60°, ta cũng áp dụng công thức tính thể tích khối lăng trụ: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Diện tích đáy và chiều cao đã được tính tương tự như phần a), ta có thể tính được thể tích khối lăng trụ ABC.ABC.

Đáp án A
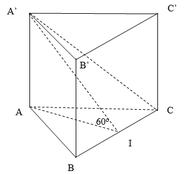
Ta có:
A I = 2 a 2 − a 2 = a 3 ; A A ' = A I tan 60 ° = a 3 . 3 = 3 a
Thể tích lăng trụ là:
V = A A ' . S A B C = 3 a . 1 2 2 a 2 sin 60 ° = 3 3 a 3

Đáp án A
Gọi H là trung điểm của BC, giao điểm của (P) và A A ' là P.
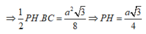

∆ A H P vuông tại P có A P = A H 2 - P H 2 = 3 a 4
∆ A A ' O ~ ∆ A H P ⇒ A ' O A O = H P A P
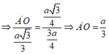
⇒ V A B C . A ' B ' C ' = O A ' . S A B C = a 3 3 12
Đáp án C