Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

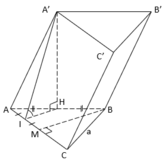
Gọi H, M, I lần lượt là trung điểm của các đoạn thẳng AB, AC, AM.
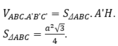
Ta có IH là đường trung bình của tam giác AMB, MB là trung tuyến của tam giác đều ABC.
Do đó:
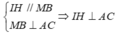
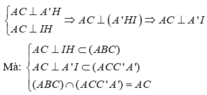
⇒ A ' I H ^ là góc gữa hai mặt phẳng (AA'C'C) và (ABCD)
⇒ A ' I H ^ = 45 °
Trong tam giác A'HI vuông tại H, ta có:


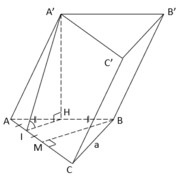
Gọi H, M, I lần lượt là trung điểm của các đoạn thẳng AB, AC, AM.

Ta có IH là đường trung bình của tam giác AMB, MB là trung tuyến của tam giác đều ABC.
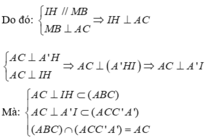
![]()
![]()
Trong tam giác A'HI vuông tại H, ta có:
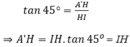
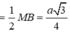
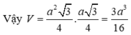

Đáp án D
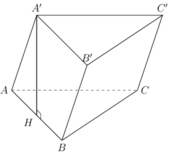
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8

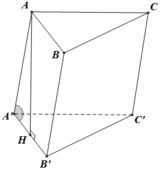
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và \(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam gaics vuông AA'H:
\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{3a}{2}\)
\(V=A'A.S_{ABC}=\dfrac{3a}{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{3}}{8}\)
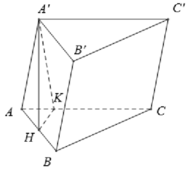



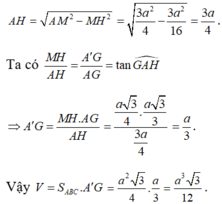

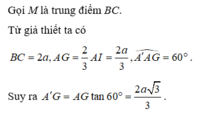
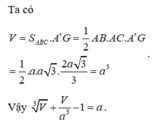
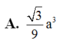
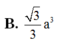
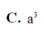


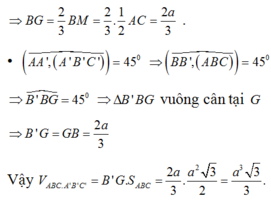
Đáp án B