Một dãy phố có 5 cửa hàng bán quần áo. Có 5 người khách đến mua quần áo, mỗi người khách vào ngẫu nhiên một trong 5 cửa hàng đó. Xác suất để có ít nhất một cửa hàng có nhiều hơn 2 người khách vào bằng
A. 181 625
B. 24 625
C. 32 125
D. 21 625
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố: Có 3 người cùng đến quầy thứ nhất .
Số kết quả thuận lợi của biến cố A là: ![]()
Xác suất của biến cố A: 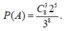

Mỗi người khách có 3 cách chọn quầy nên không gian mẫu là: \(3^8\)
Chọn 3 người khách từ 8 người: \(C_8^3\) cách
Xếp 3 người đó vào quầy 1 có 1 cách, còn lại 5 người khách xếp vào 2 quầy còn lại, mỗi người khách có 2 cách chọn quầy nên 5 người này có \(2^5\) cách chọn quầy
\(\Rightarrow C_8^3.1.2^5\) cách để 3 người đến quầy thứ nhất

Giá chiếc áo trước lần giảm giá 2 là:
304000:95%=320000(đồng)
Giá chiếc áo ban đầu là:
320000:80%=400000(đồng)
Đáp án A
Số phần tử của không gian mẫu
*Gọi A là biến cố cần tính xác suất;
theo giả thiết bài toán chỉ có một cửa hàng mà có số khách vào là 3, 4 hoặc 5.
TH1: Một cửa hàng có 3 vị khách vào
+) Chọn 1 trong 5 cửa hàng có C 5 1 cách.
+) Chọn 3 trong 5 vị khách có C 5 3 cách.
+) 3 khách vừa chọn sẽ vào cửa hàng vừa chọn ở trên có 1 cách.
+) 2 khách còn lại mỗi khách có 4 lựa chọn nên có 4 2 cách.
Vậy trường hợp này có C 5 1 . C 5 3 . 4 2 cách.
TH2: Một cửa hàng có 4 vị khách vào, có tất cả C 5 1 . C 5 4 . 4 cách.
TH3: Một cửa hàng có 5 vị khách vào, có tất cả C 5 1 . C 5 5 cách.
Xác suất cần tính