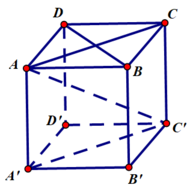
Cho hình lập phương ABCD.A’B’C’D’
a) Hãy phân tích các vecto A C ' → v à B D → theo ba vecto A B → , A D → , A A ' →
b) Tính cos A C ' → , B D → và từ đó suy ra A C ' → v à B D → vuông góc với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\overrightarrow{u}-\overrightarrow{v}\)

\(\overrightarrow{AF}=\overrightarrow{AE}+\overrightarrow{AB}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AF}-\overrightarrow{AC}+\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AB}-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AF}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AH}\)

ABCD là hbh \(\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\)
Ta có:
\(\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BD}\Rightarrow\overrightarrow{AD}-\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow2\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}=\dfrac{1}{2}\overrightarrow{a}+\dfrac{1}{2}\overrightarrow{b}\)

Sai thì thôi nha :>
Theo đề ra: ABCD là hình bình hành
\(vectoAD+vectoAB=vectoAC\) và \(vectoAB+vectoAC=vectoBD\)
\(\Leftrightarrow vectoAD=-vectoAB+vectoAC\)
\(\Leftrightarrow vectoAD=vectoAB+vectoAC-2vectoAB=vectoBD-2vectoAB=b-2a\)
\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
suy ra \(2\overrightarrow{AD}=\overrightarrow{BD}+\overrightarrow{AC}\Leftrightarrow\overrightarrow{AD}=\frac{\overrightarrow{BD}+\overrightarrow{AC}}{2}=\frac{a+b}{2}\).

\(\overrightarrow{m}=2\overrightarrow{a}+3\overrightarrow{b}-\overrightarrow{c}=2\left(3;2\right)+3\left(-4;7\right)-\left(5;0\right)=\left(2.3-3.4-5;2.2+3.7+0\right)=\left(-11;25\right)\)
\(\overrightarrow{a}=x.\overrightarrow{b}+y.\overrightarrow{c}\) \(\Rightarrow\left\{{}\begin{matrix}3=-4x+5y\\2=7x+0.y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{-11}{28}\\y=\dfrac{2}{7}\end{matrix}\right.\)
Vậy \(\overrightarrow{a}=\dfrac{-11}{28}\overrightarrow{b}+\dfrac{2}{7}\overrightarrow{c}\)
Tương tự câu trên: \(\overrightarrow{c}=x.\overrightarrow{a}+y.\overrightarrow{b}\) \(\Rightarrow\left\{{}\begin{matrix}5=3x-4y\\0=2x+7y\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{35}{29}\\y=\dfrac{-10}{29}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{c}=\dfrac{35}{29}\overrightarrow{a}-\dfrac{10}{29}\overrightarrow{b}\)
Quên còn biểu biễn b chưa làm, thôi bạn tự làm nốt, nó y hệt thôi, cứ việc bấm máy giải hệ 3s là xong