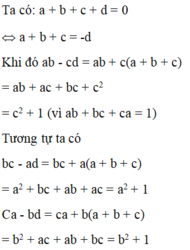Cho các số a,b,c thỏa mãn 1≥a,b,c≥0. CMR: a + b2 + c3 - ab - bc - ca ≤ 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TQ
Trần Quốc Khanh
24 tháng 4 2020
Đúng(0)
Những câu hỏi liên quan
HL
2
30 tháng 6 2019
Ta có : \(a+b+c=3\Rightarrow\left(a+b+c\right)^2=9\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^2+b^2+c^2=9-2\left(ab+bc+ca\right)=9-2\times6=3\)
\(\Rightarrow a^2+b^2+c^2=ab+bc+ca\)
\(\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Rightarrow a=b=c\)
Mà \(a+b+c=3\Rightarrow a=b=c=1\)
\(\Rightarrow A=\left(1-1\right)^{2019}+\left(1^2-1\right)^{2020}+\left(1^3-1\right)^{2021}\)
\(=0^{2019}+0^{2020}+0^{2021}=0\)
NA
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
TD
0
25 tháng 7 2021
Bài 2 :
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
<=> a^2 + b^2 + c^2 + 2ab + 2bc + 2ca = 3ab + 3bc + 3ca
<=> a^2 + b^2 + c^2 = ab + bc + ca
<=> 2a^2 + 2b^2 + 2c^2 = 2ab + 2bc + 2ca
<=> ( a - b )^2 + ( b - c )^2 + ( c - a )^2 = 0
<=> a = b = c
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
1.
\(\Leftrightarrow2a^2+2b^2+18=2ab+6a+6b\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-6a+9\right)+\left(b^2-6b+9\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-3\right)^2+\left(b-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-3=0\\b-3=0\end{matrix}\right.\) \(\Leftrightarrow a=b=3\)
2.
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c\)
TA
0
24 tháng 6 2021
Đặt A = \(\dfrac{a-b}{1+c^2}+\dfrac{b-c}{1+a^2}+\dfrac{c-a}{1+b^2}=0\)
= \(\dfrac{a-b}{c^2+ab+bc+ca}+\dfrac{b-c}{a^2+ab+bc+ca}+\dfrac{c-a}{b^2+ab+bc+ca}\)
= \(\dfrac{a-b}{\left(c+a\right)\left(c+b\right)}+\dfrac{b-c}{\left(a+b\right)\left(c+a\right)}+\dfrac{c-a}{\left(a+b\right)\left(b+c\right)}\)
= \(\dfrac{\left(a-b\right)\left(a+b\right)+\left(b-c\right)\left(b+c\right)+\left(c+a\right)\left(c-a\right)}{\left(c+a\right)\left(b+c\right)\left(a+b\right)}\)
= \(\dfrac{a^2-b^2+b^2-c^2+c^2-a^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
AT
24 tháng 6 2021
\(\dfrac{a-b}{1+c^2}+\dfrac{b-c}{1+a^2}+\dfrac{c-a}{1+b^2}\)
\(=\dfrac{a-b}{ab+bc+ca+c^2}+\dfrac{b-c}{ab+bc+ca+a^2}+\dfrac{c-a}{ab+bc+ca+b^2}\)
\(=\dfrac{a-b}{\left(c+a\right)\left(c+b\right)}+\dfrac{b-c}{\left(a+b\right)\left(a+c\right)}+\dfrac{c-a}{\left(b+a\right)\left(b+c\right)}\)
\(=\dfrac{\left(a-b\right)\left(a+b\right)+\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
\(=\dfrac{a^2-b^2+b^2-c^2+c^2-a^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 1 2022
\(P=\dfrac{a^2+b^2+c^2}{ab+bc+ca}\ge\dfrac{ab+bc+ca}{ab+bc+ca}=1\)
\(P_{min}=1\) khi \(a=b=c=1\)
\(P=\dfrac{\left(a+b+c\right)^2-2\left(ab+bc+ca\right)}{ab+bc+ca}=\dfrac{9}{ab+bc+ca}-2\)
Do \(a;b\ge1\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\Rightarrow ab\ge a+b-1=2-c\)
\(\Rightarrow ab+c\left(a+b\right)\ge2-c+c\left(3-c\right)=-c^2+2c+2=c\left(2-c\right)+2\ge2\)
\(\Rightarrow P\le\dfrac{9}{2}-2=\dfrac{5}{2}\)
\(P_{max}=\dfrac{5}{2}\) khi \(\left(a;b;c\right)=\left(1;2;0\right);\left(2;1;0\right)\)
T
24 tháng 9 2015
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).Vậy điều giả sử trên là sai,
a,b,c là 3 số dương.
24 tháng 9 2015
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).
Vậy điều giả sử trên là sai,
Do đó a,b,c là 3 số dương.
