Cho tứ diện SABC có tam giác ABC vuông tại B; SA ⊥ (ABC)
a) Chứng minh : BC ⊥ (SAB)
b) Gọi AH là đường cao của ΔSAB. Chứng minh : AH⊥SC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (SB;(ABC))=(SB;BA)=góc SBA
\(\tan SBA=\dfrac{SA}{AB}=\sqrt{6}\)
=>góc SBA=68 độ
b: (SA;(SBC))=(SA;SB)=góc ASB
tan ASB=AB/SA=1/căn 6
=>góc ASB=22 độ

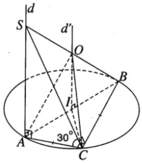
Gọi I là trung điểm của cạnh AB. Vì tam giác ABC vuông cân tại C nên ta có IA = IB = IC. Vậy I là tâm đường tròn ngoại tiếp tam giác ABC. Do đó, tâm mặt cầu ngoại tiếp tứ diện SABC phải nằm trên đường thẳng d’ vuông góc với mặt phẳng (ABC) tại I. Ta suy ra d’ // d. Do đó d’ cắt SB tại trung điểm O của đoạn SB. Ta có OB = OS = OA = OC và như vậy O là tâm đường tròn ngoại tiếp tứ diện SABC.

Gọi E là trung điểm của AB, ta có ME song song với CN và ME = 1/2 AC = CN. Vậy tam giác MEC và tam giác NCB đồng dạng với tỉ số 1:2. Từ đó, ta có:
• Diện tích tam giác MEC là 1/4 diện tích tam giác ABC, hay S_MEC = 1/4 S_ABC = 42cm^2.
• Diện tích tam giác NCB là 3/4 diện tích tam giác ABC, hay S_NCB = 3/4 S_ABC = 126cm^2.
Gọi F là trung điểm của BC, ta có EF song song với DM và EF = 1/2 IB = AL. Vậy tứ giác DMNB và tứ giác AEFB đồng dạng với tỉ số 1:2. Từ đó, ta có:
• Diện tích tứ giác AEFB là 1/2 diện tích tứ giác ABCD, hay S_AEFB = 1/2 S_ABCD = 84cm^2.
• Diện tích tứ giác DMNB là 1/2 diện tích tứ giác AEFB, hay S_DMNB = 1/2 S_AEFB = 42cm^2.
Vậy diện tích tam giác BNC là 126cm^2 và diện tích tứ giác DMNB
là 42cm^2.

SA vg (ABC)=> SAB,SAC vuông
SA vg BC, AB vg BC => BCvg (SAB) =>SB vg BC=> SBC vuông
vậy all mặt đều vuông
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\AB\subset\left(ABC\right)\end{cases}}\) \(\Rightarrow SA\perp AB\Rightarrow\) tam giác SAB vuông (1)
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\AC\subset\left(ABC\right)\end{cases}\Rightarrow AC\perp SA\Rightarrow}\) tam giác SAC vuông (2)
Tam giác ABC vuông tại B (gt) (3)
\(\Rightarrow AB\perp BC\)
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\BC\subset\left(ABC\right)\end{cases}\Rightarrow SA\perp BC}\)
\(\hept{\begin{cases}AB\perp BC\\SA\perp BC\end{cases}\Rightarrow\hept{\begin{cases}BC\perp\left(SAB\right)\\SB\subset\left(SAB\right)\end{cases}\Rightarrow}SB\perp BC\Rightarrow}\) Tam giác SBC vuông (4)
\(\left(1\right);\left(2\right);\left(3\right);\left(4\right)\Rightarrowđpcm\)


Vậy \(SB^2=\dfrac{6a^2}{9}+4a^2=\dfrac{42a^2}{9}\)
Do đó \(SB=\dfrac{a\sqrt{42}}{3}\)
Ta suy ra :
\(r=\dfrac{SB}{2}=\dfrac{a\sqrt{42}}{6}\)
a. Ta có: \(\left\{{}\begin{matrix}AB\perp BC\\SA\perp BC\end{matrix}\right.\)\(\Rightarrow BC\perp\left(SAB\right)\)
b. Ta có: \(\left\{{}\begin{matrix}AH\perp SB\\AH\perp BC\:\left(BC\perp\left(SAB\right)\right)\end{matrix}\right.\)\(\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH\perp SC\)