Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
6CO2 + 6H2O + 2813kJ → C6H12O6 + 6O2 || nglucozơ = 0,01 mol
⇒ năng lượng cần cung cấp là 0,01 × 2813 × 103 = 28130J.
Năng lượng 10 lá cây nhận được mỗi phút = 10 × 10 × 2,09 × 0,1 = 20,9J.
► Thời gian để tạo ra 1,8 gam glucozơ = 28130 ÷ 20,9 = 1346 phút

Đáp án: A
n este = 1/2.nNaOH ; mà n muối = n rượu = n este
=> Este hai chức, tạo từ axit hai chức và rượu 2 chức, mạch thẳng


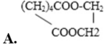
Chọn đáp án D.
Quy đổi hỗn hợp T tương đương với hỗn hợp gồm CnH2n+2O (x mol); CmH2m-6O6 (y mol).
n
C
O
2
=
a
n
H
2
O
=
a
+
0
,
03
→
B
T
K
L
26
,
86
+
32.1
,
425
=
44
a
+
18.
a
+
0
,
03
⇒
a
=
1
,
16
→
B
T
N
T
O
x
+
6
y
=
2.1
,
16
+
0
,
03
+
1
,
16
−
2.1
,
425
=
0
,
66
m
o
l
1
14
n
+
18
x
+
14
m
+
90
y
=
26
,
86
g
⇒
14.
n
x
+
m
y
+
18
x
+
90
y
=
14.1
,
16
+
18
x
+
90
y
=
26
,
86
2
Từ (1) và (2) suy ra:
x
=
0
,
24
y
=
0
,
07
Ancol + K dư:
∑
n
a
n
c
o
l
=
3
n
e
s
t
e
+
n
a
n
c
o
l
=
2
n
H
2
=
2.0
,
18
=
0
,
36
m
o
l
n
e
s
t
e
=
0
,
36
−
0
,
24
3
=
0
,
04
m
o
l
⇒
n
a
x
i
t
=
0
,
07
−
0
,
04
=
0
,
03
m
o
l
Ancol + AgNO3/NH3 dư:
n
A
g
=
129
,
6
108
=
1
,
2
m
o
l
⇒
2
<
n
A
g
∑
n
a
n
c
o
l
=
1
,
2
0
,
36
<
4
Þ Chứng tỏ A là CH3OH, kí hiệu ancol B, C là RCH2OH
⇒ ∑ n a n c o l = n C H 3 O H + n R C H 2 O H = 0 , 36 m o l n A g = 4 n C H 3 O H + 2 n R C H 2 O H = 1 , 2 m o l ⇒ n C H 3 O H = 0 , 24 m o l n R C H 2 O H = 0 , 12 m o l
Vậy T gồm: C H 3 O H : 0 , 24 − 0 , 04 = 0 , 2 m o l R C H 2 O H : 0 , 12 − 0 , 04.2 = 0 , 04 m o l a x i t : 0 , 03 m o l e s t e : 0 , 04 m o l
Bảo toàn nguyên tố C: 0 , 2.1 + 0 , 04. C B , C + 0 , 04. C D + 1 + 2 C B , C + 0 , 03. C D = 1 , 16
⇒ 0 , 12 C B , C + 0 , 07 C D = 0 , 92
C B , C > 2 ⇒ C D < 0 , 92 − 0 , 12.2 0 , 07 = 9 , 7 m à C D ≥ 8
⇒ C D = 8 C D = 9 ⇒ D : C 8 H 10 O 6 D : C 9 H 12 O 6 ⇒ % m D = 202.0 , 03 26 , 86 .100 % = 22 , 56 % % m D = 216.0 , 03 26 , 86 .100 % = 24 , 13 %

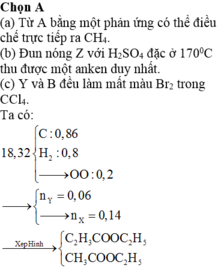
Chọn đáp án A
Ta có: 18,32 C : 0 , 86 H 2 : 0 , 8 → O O : 0 , 2 → n Y = 0 , 06 → n X = 0 , 14 → x e p h i n h C 2 H 3 C O O C 2 H 5 C H 3 C O O C 2 H 5
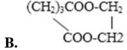
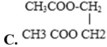
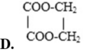



Vậy \(SB^2=\dfrac{6a^2}{9}+4a^2=\dfrac{42a^2}{9}\)
Do đó \(SB=\dfrac{a\sqrt{42}}{3}\)
Ta suy ra :
\(r=\dfrac{SB}{2}=\dfrac{a\sqrt{42}}{6}\)