Cho hàm số \(y=f\left(x\right)=ax+\frac{8}{9}\).Tính các giá trị của a,biết rằng đồ thị hàm số đi qua điểm M(a+2;\(3a^2+2a\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1 2022
Bài 9:
b: Điểm A thuộc đồ thị vì \(y_A=4=-2\cdot\left(-2\right)=-2\cdot x_A\)
Bài 10:
a: Thay x=1 và y=-3 vào (d), ta được:
\(a\cdot1=-3\)
hay a=-3
9 đko nhỉ
CM
27 tháng 12 2017
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:
11 = 3.4 + b = 12 + b
=> b = 11 – 12 = -1
Ta được hàm số y = 3x – 1
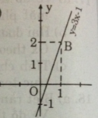
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5
=> a = 5 – 3 = 2
Ta được hàm số y = 2x + 5.
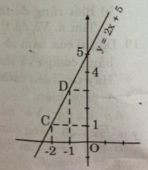
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
8 tháng 4 2022
Bài 2:
\(3x^2+5\ge5>0\forall x\)
nên f(x)>0 với mọi x
TN
27 tháng 5 2019
Ta có: 2x+y=3 \(\Leftrightarrow\) y=-2x-3
a) Vì hs y=ax+b song song với đt y=-2x-3 nên\(\hept{\begin{cases}a=-2\\b\ne-3\end{cases}}\)
Suy ra pt y = ax + b là y = -2x + b (b\(\ne\)-3)
Mặt khác đt này lại đi qua điểm M(2;5) nên khi x=2 thì y=5. Ta có phương trình:
-2.2+b=5 \(\Leftrightarrow\)-4+b=5 \(\Leftrightarrow\) b=9
Vậy.......
- Thay \(x=a+2,y=3a^2+2a\) vào hàm số f(X) ta được :
\(3a^2+2a=a\left(a+2\right)+\frac{8}{9}\)
=> \(3a^2+2a=a^2+2a+\frac{8}{9}\)
=> \(3a^2+2a-a^2-2a-\frac{8}{9}=0\)
=> \(2a^2-\frac{8}{9}=0\)
=> \(a^2=\frac{4}{9}\)
=> \(\orbr{\begin{cases}a=-\frac{2}{3}\\a=\frac{2}{3}\end{cases}}\)
Vậy a có các giá trị là \(a=-\frac{2}{3},a=\frac{2}{3}\)