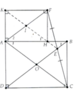
Cho hình chữ nhật ABCD . Nối C với E điểm bất kì trên đường BD . Trên tia đối của EC lấy điểm F sao cho EF = EC . Vẽ FH và FK lần lượt vuông góc với AB và AD .
a) CM tứ giác AHFK là hình chữ nhật
b) CM AF song song BD
c) CM 3 điểm EHK thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 5 2018
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
12 tháng 11 2021
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
a)Xét tứ giác AHFK có góc AHF=90(gt), góc HAK=90(gt), góc AKF=90(gt)
=> tứ giác AHFK là hcn
b) Gọi O là giao điểm của AC và BD, M là giao điểm của HK và AF
Xét tam giác CAF có CO=OA(gt), CE=EF(gt)
=>OE là đường trung bịnh của tam giác CÀ
=>OE//AF hay BD//AF
Ta có OA=OD(ABCD là hcn)
=> tam giác OAD cân tại O
=>góc OAD=góc ODA
Mà góc ODA=góc FAD(so le trong)
=>góc OAD=góc FAD hay góc CAD=góc MAK(1)
Ta lại có MA=MK(AHFK là hcn)
=>tam giác MAK cân tại M
=>góc MAK= góc MKA(2)
Từ (1) và (2)=>góc CAD=góc MKA hay góc CAD=góc HKA
=>AC//HK(có cặp góc slt bằng nhau)
c)Xét tam giác FAC có FM=MA(AHFK là hcn), FE=EC(gt)
=>ME là đường trung bình của tam giác FAC
=>ME//AC(3)
Mà HK//AC(cmt)(4)
Mặt khác M thuộc AC(5)
Từ (3),(4) và (5)=> H,K,E thẳng hàng