cho tam giác nhọn abc gọi h là trực tâm của tam giác gọi K là điểm đối xứng với H qua ABC tìm liên hệ giữa số đo các góc BAC và BKC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 11 2021
a) Ta có:
K đối xứng với H qua BC
⇒ BC là trung trực của HK
⇒ BH=BK; CH=CK
Xét ΔBHC và ΔBKC có:
BH=BK (cmt)
CH=CK (cmt)
BC: cạnh chung
Do đó ΔBHC = ΔBKC(c.c.c)
b) Ta có:
ˆBHK = ˆBAH + ˆABH (góc ngoài của ΔABH)
ˆCHK = ˆCAH+ ˆACH (góc ngoài của ΔACH)
⇒ ˆBHC = ˆBHK + ˆCHK
= ˆBAH + ˆABH + ˆCAH + ˆACH
= ˆBAC + ˆABH + ˆACH
Ta lại có:
ˆBAC+ˆABH = 90o (BH⊥AC)
ˆBAC+ˆACH = 90o (CH⊥AB)
⇒2ˆBAC+ˆABH+ˆACH=180o
⇒ˆABH+ ˆACH = 180o− 2ˆBAC
Do đó:
ˆBHC =ˆBAC+ 180o− 2ˆBAC= 180o− ˆBAC= 180o−70o = 110o
Mặt khác:
ˆBHC = ˆBKC (ΔBHC = ΔBKC)
⇒ˆBKC=110
30 tháng 8 2021
a: Ta có: H và K đối xứng nhau qua BC
nên BC là đường trung trực của HK
Suy ra: BH=BK và CH=CK
Xét ΔBHC và ΔBKC có
BH=BK
BC chung
HC=KC
Do đó: ΔBHC=ΔBKC
CM
31 tháng 1 2017
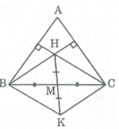
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK, ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
Ta có: CH ⊥ AB (gt)
Suy ra: KB ⊥ AB nên ∠ (KBA) = 90 0
Ta có: BH ⊥ AC (gt)
Suy ra: CK ⊥ AC nên ∠ (KCA) = 90 0
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 7 2021
Xet tứ giác BHCK có
MH=MK; MB=MC => BHCK là hình bình hành (Tứ giác có các cặp cạnh đối cắt nhau tại trung điểm mỗi đường là hbh)
=> CK//BH mà BH vuông góc với AC => CK vuông góc với AC => \(\widehat{ACK}=90^o\)
=> BK//CH mà CH vuông góc với AB => BK vuông góc với AB => \(\widehat{ABK}=90^o\)
Đáp án:
ˆBKC=110oBKC^=110o
Giải thích các bước giải:
a) Ta có:
KK đối xứng với HH qua BCBC
⇒BC⇒BC là trung trực của HKHK
⇒BH=BK;CH=CK⇒BH=BK;CH=CK
Xét ΔBHC∆BHC và ΔBKC∆BKC có:
BH=BK(cmt)BH=BK(cmt)
CH=CK(cmt)CH=CK(cmt)
BC:BC: cạnh chung
Do đó ΔBHC=ΔBKC(c.c.c)∆BHC=∆BKC(c.c.c)
b) Ta có:
ˆBHK=ˆBAH+ˆABHBHK^=BAH^+ABH^ (góc ngoài của ΔABH∆ABH)
ˆCHK=ˆCAH+ˆACHCHK^=CAH^+ACH^ (góc ngoài của ΔACH∆ACH)
⇒ˆBHC=ˆBHK+ˆCHK⇒BHC^=BHK^+CHK^
=ˆBAH+ˆABH+ˆCAH+ˆACH=BAH^+ABH^+CAH^+ACH^
=ˆBAC+ˆABH+ˆACH=BAC^+ABH^+ACH^
Ta lại có:
ˆBAC+ˆABH=90oBAC^+ABH^=90o (BH⊥AC)(BH⊥AC)
ˆBAC+ˆACH=90oBAC^+ACH^=90o (CH⊥AB)(CH⊥AB)
⇒2ˆBAC+ˆABH+ˆACH=180o⇒2BAC^+ABH^+ACH^=180o
⇒ˆABH+ˆACH=180o−2ˆBAC⇒ABH^+ACH^=180o−2BAC^
Do đó:
ˆBHC=ˆBAC+180o−2ˆBAC=180o−ˆBAC=180o−70o=110oBHC^=BAC^+180o−2BAC^=180o−BAC^=180o−70o=110o
Mặt khác:
ˆBHC=ˆBKC(ΔBHC=ΔBKC)BHC^=BKC^(∆BHC=∆BKC)
⇒ˆBKC=110o