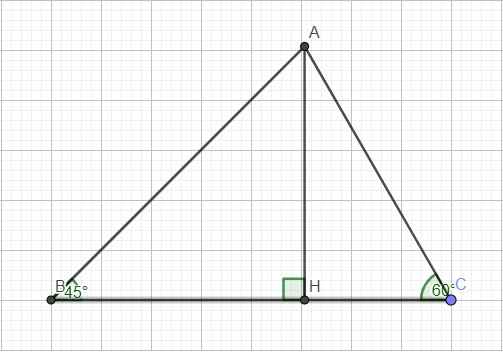
Tính SABC biết BC= 2cm , góc A = 105 độ , góc C= 30 độ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2016
kẻ đường cao AH đặt AH=x
tam giác AHB có góc AHB=90 độ=>góc HAB=góc HBA=45 độ
=>tam giác AHB vuông cân tại H=>BH=AH=x
tam giác AHC vuông tại H=> \(AC^2=AH^2+HC^2=x^2+\left[2-x\right]^2\)[1]
tam giác AHC có góc H=90độ góc C=30 độ => góc HAC=60 độ=> \(HC=\frac{AC.\sqrt{3}}{2}suyraAC=\frac{2HC}{\sqrt{3}}suyraAC^2=\frac{4HC^2}{3}\)[2]
[1,2]=>\(x^2+\left[2-x\right]^2=\frac{4\left[2-x\right]^2}{3}\)
giải phương trình =>x=\(\sqrt{3}-1\)
Sabc=1/2.BC.AH=\(\frac{1}{2}.2.\left[\sqrt{3}-1\right]=\sqrt{3}-1cm^2\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ABH ta có:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH ta có:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{\left(2a\right)^2}{2\left(cot45^0+cot60^0\right)}=\left(3-\sqrt{3}\right)a^2\)
1 tháng 5 2020
Trả lời :
Bạn Nguyễn Khánh Huyền đừng bình luận linh tinh nhé.
- Hok tốt !
^_^
1 tháng 5 2020
bạn nguyễn thị khánh huyền ơi đừng lấy ảnh của mk đi bình luận linh tinh nhé
ko hay đâu bạn ơi
