Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
Chứng minh rằng AK=KC,BI=ID
vì FE là đường trung bình hình thang nên FE//AB//CD
E, F là trung điểm của AD và BC nên AK=KC
BI=ID
( trong tam giác đường thẳng qua trung điểm của 1 cạnh, // với cạnh thứ 2 thì qua trung điểm cạnh thứ 3)
Xét t/g ABC và t/g CDA có :
AC cạnh chung
AB = CD ( gt )
\(\widehat{A1}=\widehat{C1}\)( slt , AB // CD )
\(\Rightarrow\)t/g ABC = t/g CDA ( c-g-c )
\(\Rightarrow\)BC = AD
\(\widehat{A2}=\widehat{C2}\) và 2 góc này ở vị trí slt
\(\Rightarrow\)BC // AD
b: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD;AD//BC
\(\text{AB song song với CD và AB=CD}\Rightarrow ABCD\text{ là hình bình hành}\)
\(\Rightarrow AD\text{//}BC\text{ và }AD=BC\)
Xét tứ giác ABCD có
AB//CD
AD//BC
DO đó: ABCD là hình bình hành
Suy ra: AB=CD; AD=BC
AB=BM
nên \(S_{QAB}=S_{QBM}\)
DA=AQ
=>\(S_{BDA}=S_{BAQ}\)
=>\(S_{QAM}=2\cdot S_{ABD}\)
Tương tự, ta được: \(S_{MBN}=2\cdot S_{ABC};S_{NCP}=2\cdot S_{BCD};S_{PDQ}=2\cdot S_{ADC}\)
=>\(S_{MNPQ}=5\cdot S_{ABCD}=300\left(cm^2\right)\)
Bạn ơi có đáp án câu này không mình xin với. Mình cũng đang học
và 
. 
và 
. 
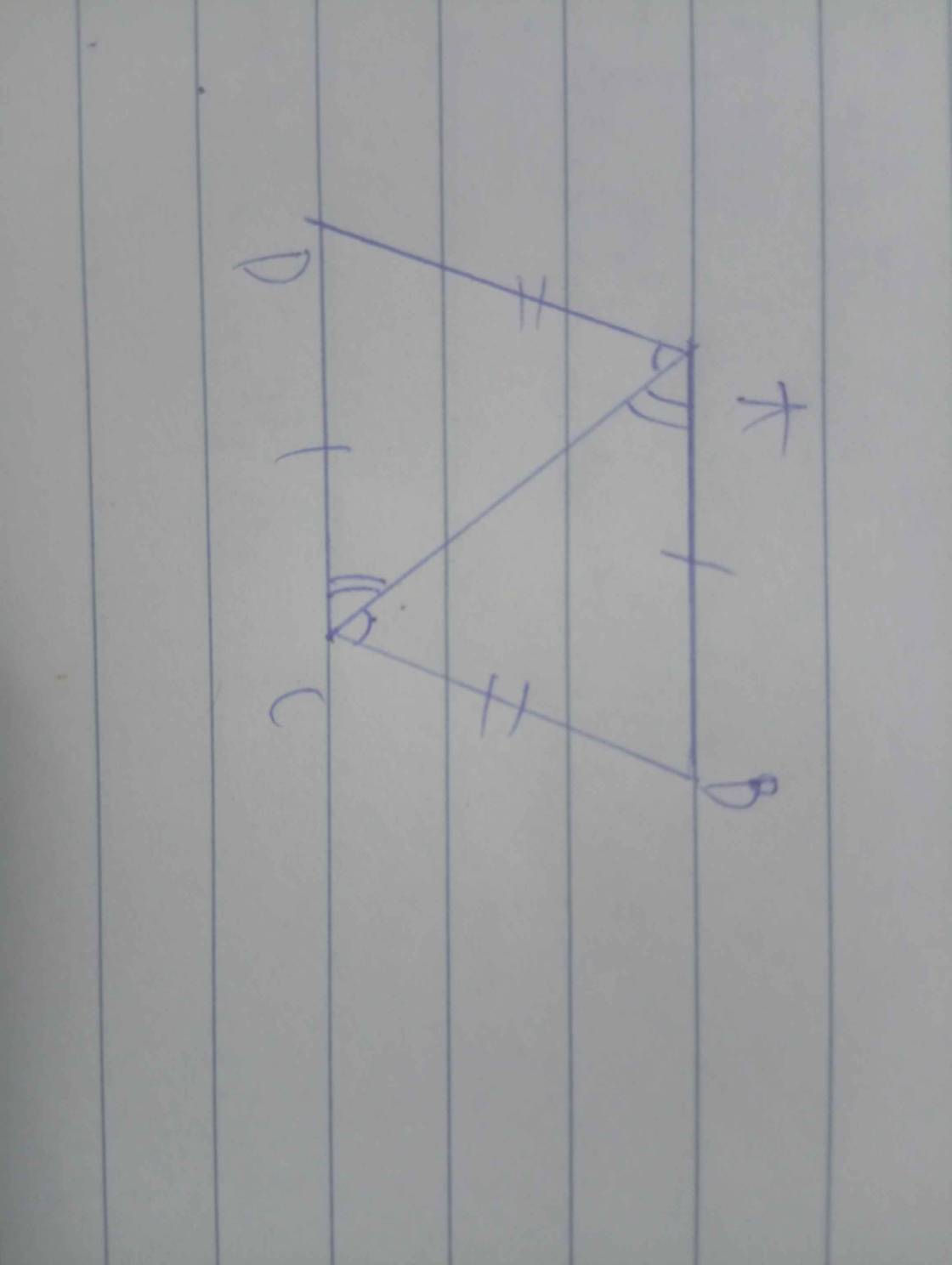
* Hướng dẫn câu b:
Gọi I là giao điểm của Gx và PQ. Kéo dài PQ cắt hai cạnh AD và BC theo thứ tự là E và F.
Góc MPQ = góc GEF (so le trong do MP // AD)
Góc MQP = góc GFE (so le trong do MQ // BC)
góc MPQ = góc MQP (tam giác MPQ cân do MP = MQ)
=> góc GEF = góc GEF -> tam giác GEF cân tại G
mà GI là phân giác của góc G -> GI vuông góc với EF
-> Gx vuông góc với PQ -> Gx // MN (MN vuông góc với PQ do hình thoi có 2 đường chéo vuông góc).
Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
Ví dụ :
B(5) = {5.1, 4.2, 5.3, …} = {5, 10, 15, …}
Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.