Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD;AD//BC

Chứng minh rằng AK=KC,BI=ID
vì FE là đường trung bình hình thang nên FE//AB//CD
E, F là trung điểm của AD và BC nên AK=KC
BI=ID
( trong tam giác đường thẳng qua trung điểm của 1 cạnh, // với cạnh thứ 2 thì qua trung điểm cạnh thứ 3)
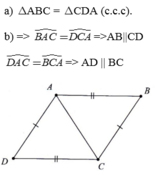
Xét t/g ABC và t/g CDA có :
AC cạnh chung
AB = CD ( gt )
\(\widehat{A1}=\widehat{C1}\)( slt , AB // CD )
\(\Rightarrow\)t/g ABC = t/g CDA ( c-g-c )
\(\Rightarrow\)BC = AD
\(\widehat{A2}=\widehat{C2}\) và 2 góc này ở vị trí slt
\(\Rightarrow\)BC // AD




a) \(AB^2+CD^2=OA^2+OB^2+OC^2+OD^2=\left(OA^2+OD^2\right)+\left(OB^2+OC^2\right)=AD^2+BC^2\)b) -Áp dụng định lí:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng 1 nửa cạnh huyền.
\(OM+ON+OP+OQ=\dfrac{1}{2}AB+\dfrac{1}{2}BC+\dfrac{1}{2}CD+\dfrac{1}{2}DA=\dfrac{1}{2}\left(AB+BC+CD+DA\right)\)

1: Ta có:ABCD là hình chữ nhật
nên AB=CD;AD=BC
2: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Xét ΔADE và ΔCBF có
\(\widehat{D}=\widehat{B}\)
AD=CB
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: \(\widehat{AED}=\widehat{CFB}\)
=>\(\widehat{AEC}=\widehat{CFA}\)
Xét tứ giác AECF có
\(\widehat{AEC}=\widehat{CFA}\)
\(\widehat{FAE}=\widehat{FCE}\)
Do đó: AECF là hình bình hành
Suy ra: AE//CF
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)