Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)
a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Ta có: ΔABI=ΔACI
nên AB=AC
hay ΔABC cân tại A
c: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó:ABDC là hình bình hành
Suy ra: AB//CD
a) Xét ΔABI và ΔACI có
AB=AC(gt)
AI chung
BI=CI(I là trung điểm của BC)
Do đó: ΔABI=ΔACI(c-c-c)
b) Xét ΔAIC và ΔDIB có
IA=ID(gt)
\(\widehat{AIC}=\widehat{DIB}\)(hai góc đối đỉnh)
IC=IB(I là trung điểm của BC)
Do đó: ΔAIC=ΔDIB(c-g-c)
⇒\(\widehat{ACI}=\widehat{DBI}\)(hai góc tương ứng)(1)
mà \(\widehat{ACI}\) và \(\widehat{DBI}\) là hai góc ở vị trí so le trong
nên AC//BD(Dấu hiệu nhận biết hai đường thẳng song song)
c) Xét ΔAIB và ΔDIC có
AI=DI(gt)
\(\widehat{AIB}=\widehat{DIC}\)(hai góc đối đỉnh)
IB=IC(I là trung điểm của BC)
Do đó: ΔAIB=ΔDIC(c-g-c)
⇒AB=CD(hai cạnh tương ứng)
mà AB=AC(gt)
nên CD=AC
Xét ΔACI và ΔDCI có
CA=CD(cmt)
CI chung
IA=ID(gt)
Do đó: ΔACI=ΔDCI(c-c-c)
⇒\(\widehat{ACI}=\widehat{DCI}\)(hai góc tương ứng)
mà \(\widehat{ACI}+\widehat{DCI}=\widehat{ACD}\)(tia CI nằm giữa hai tia CA,CD)
nên \(\widehat{ACD}=2\cdot\widehat{ACI}\)(2)
Từ (1) và (2) suy ra \(\widehat{ACD}=2\cdot\widehat{DBC}\)(đpcm)
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Xét ΔABI và ΔDCI có
AI=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔABI=ΔDCI
Suy ra: AB=CD
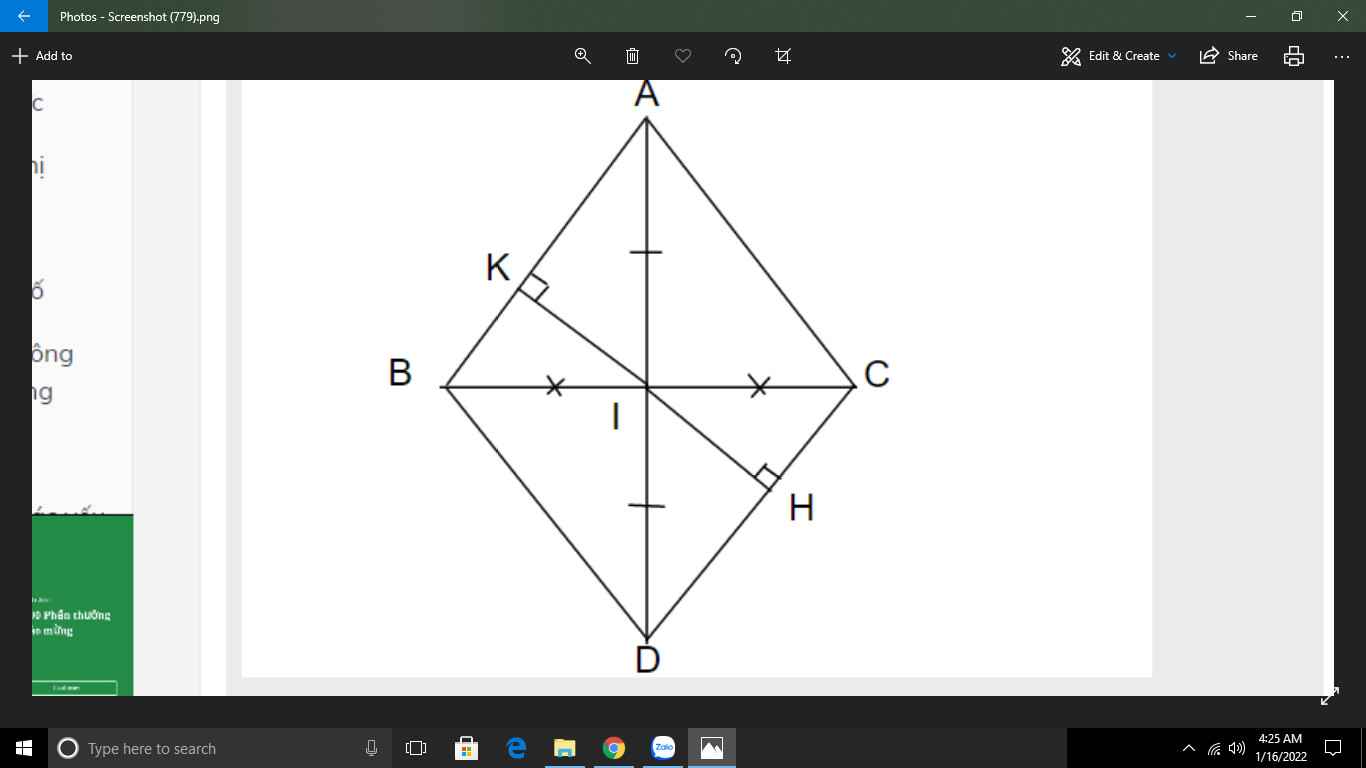
a, Xét △ABI và △ACI có :
AB = AC (gt)
BI = CI (do I là trung điểm BC)
AI chung
=> △ABI = △ACI (c-c-c)
b, Xét △AIC và △DIB có :
AI = DI (gt)
\(\widehat{AIC}=\widehat{DIB}\) (đối đỉnh)
IC = IB
=> △AIC = △DIB (c-g-c)
=> \(\widehat{DBI}=\widehat{ICA}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AC // BD
c, Xét △IKB và △IHC có :
\(\widehat{IKB}=\widehat{IHC}=90^O\)
IB = IC
\(\widehat{KIB}=\widehat{CIH}\) (đối đỉnh)
=> △IKB = △IHC (ch-gn)
=> IK = IH
con cặc