Tính giá trị biểu thức P =\(\dfrac{2^3-1}{2^3+1}\cdot\dfrac{3^3-1}{3^3+1}\cdot...\cdot\dfrac{2014^3-1}{2014^3+1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 1 2022
\(D=\left(1+\dfrac{1}{1.3}\right).\left(1+\dfrac{1}{2.4}\right)...\left(1+\dfrac{1}{2019.2021}\right)=\dfrac{4}{1.3}.\dfrac{9}{2.4}...\dfrac{2019.2021+1}{2019.2021}=\dfrac{2.2}{1.3}.\dfrac{3.3}{2.4}...\dfrac{2020.2020}{2019.2021}=\left(\dfrac{2}{1}.\dfrac{3}{2}...\dfrac{2020}{2019}\right).\left(\dfrac{2}{3}.\dfrac{3}{4}...\dfrac{2020}{2021}\right)=2020.\dfrac{2}{2021}=\dfrac{4040}{2021}\)
31 tháng 8 2021
thay b=\(\dfrac{9}{10}\) vào biểu thức,ta được:
\(\dfrac{1}{3}.\dfrac{9}{10}+\dfrac{2}{9}.\dfrac{9}{10}-\dfrac{9}{10}:\dfrac{9}{4}=\dfrac{9}{10}.\left(\dfrac{1}{3}+\dfrac{2}{9}-\dfrac{9}{4}\right)=\dfrac{9}{10}.\dfrac{-61}{36}=-\dfrac{61}{40}\)
ND
22 tháng 12 2017
a)Nhận xét
\(\dfrac{n^3+1}{n^3-1}=\dfrac{\left(n+1\right)\left(n^2-n+1\right)}{\left(n-1\right)\left(n^2+n+1\right)}=\dfrac{\left(n+1\right)\left[\left(n-0,5\right)^2+0;75\right]}{\left(n-1\right)\left[\left(n+0,5\right)^2+0,75\right]}\)
Áp dụng công thức trên:
\(A=\dfrac{2^3+1}{2^3-1}.\dfrac{3^3+1}{3^3-1}....\dfrac{9^3+1}{9^3-1}\)
\(=\dfrac{\left(2+1\right)\left[\left(2-0,5\right)^2+0,75\right]}{\left(2-1\right)\left[\left(2+0,5\right)^2+0,75\right]}.\dfrac{\left(3+1\right)\left[\left(3-0,5\right)^2+0,75\right]}{\left(3-1\right)\left[\left(3+0,5\right)^2+0,75\right]}...\dfrac{\left(9+1\right)\left[\left(9-0,5\right)^2+0,75\right]}{\left(9-1\right)\left[\left(9+0,5\right)^2+0,75\right]}\)
\(=\dfrac{3\left(1,5^2+0,75\right)}{\left(2,5^2+0,75\right)}.\dfrac{4\left(2,5^2+0,75\right)}{2\left(3,5^2+0,75\right)}...\dfrac{10\left(8,5^2+0,75\right)}{8\left(9,5^2+0,75\right)}\)
\(=\dfrac{3.4....10}{1.2.....8}.\dfrac{1,5^2+0,75}{9,5^2+0,75}\)
\(=\dfrac{9.10}{2}.\dfrac{3}{91}\)
\(=\dfrac{3}{2}.\dfrac{90}{91}< \dfrac{3}{2}\)
\(\Rightarrowđpcm\)
b) Làm tương tự
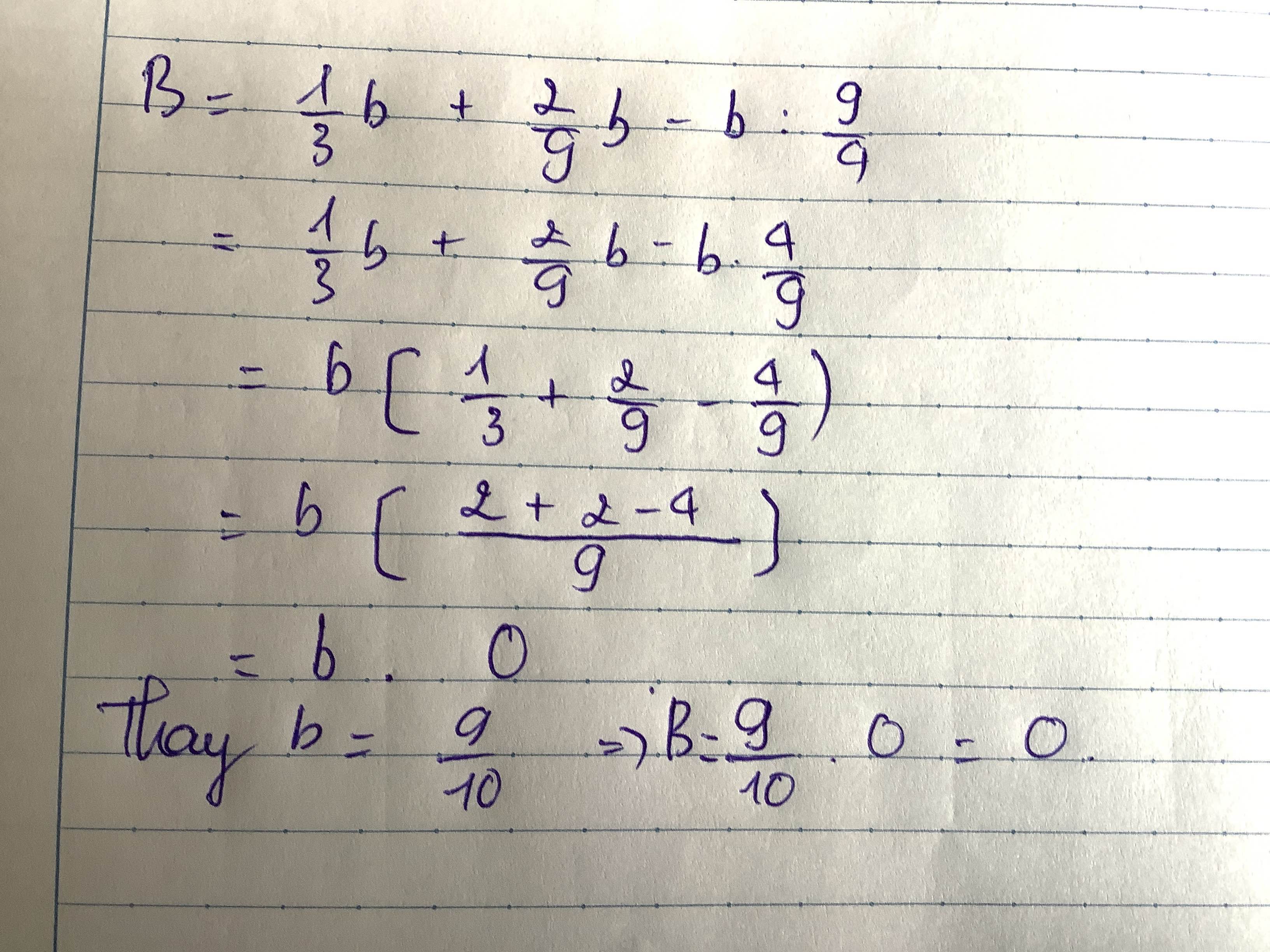
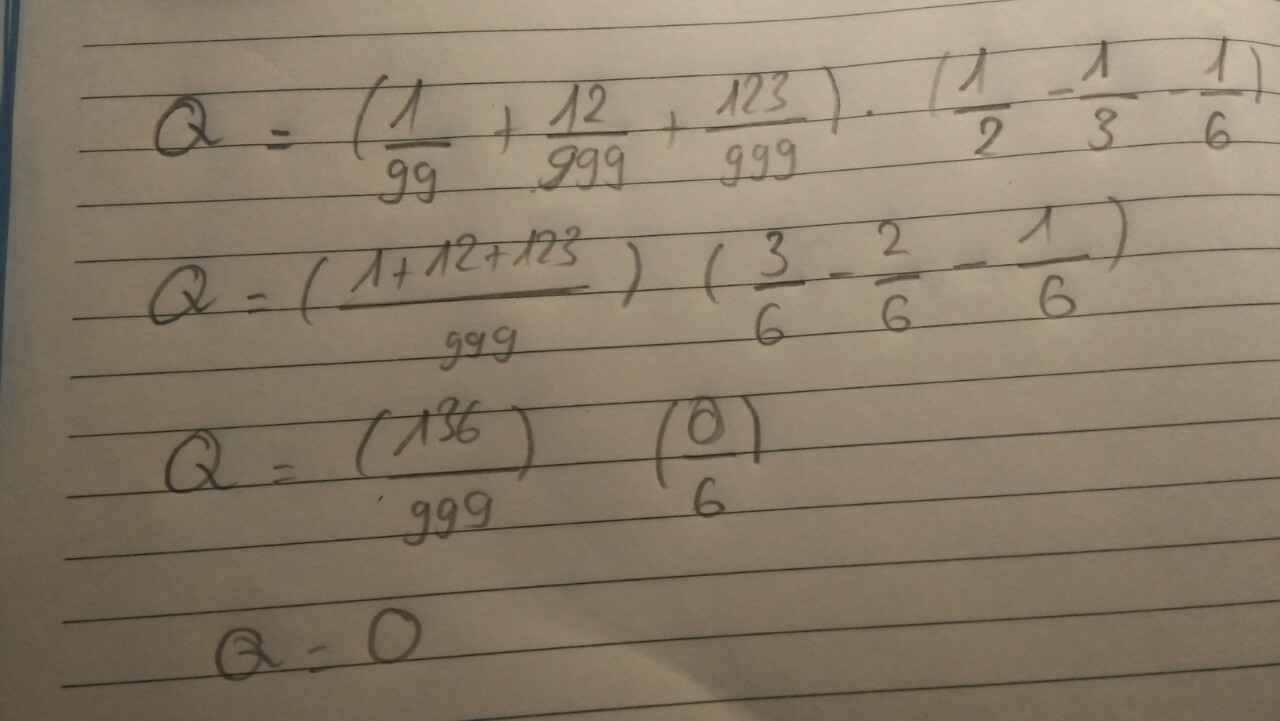
Cách làm tương tự bài dưới đây.
Câu hỏi của Nguyễn Bạch Gia Chí - Toán lớp 8 | Học trực tuyến