Ta ko có \(2^m+2^n=2^{m+n}\)
với mọi số nguyên dương n, m.Nhưng có những số nguyên dương m,n có tính chất trên. Tìm các số đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2021
\(\text{(m,n) = }\left\{\left(0;0\right);\left(1;1\right)\right\}\)
6 tháng 6 2017
Ta có :
\(2^m+2^n=2^{m+n}\Leftrightarrow2^{m+n}-2^m-2^n=0\)
\(\Leftrightarrow2^m.\left(2^n-1\right)-\left(2^n-1\right)=1\Leftrightarrow\left(2^n-1\right).\left(2^m-1\right)=1\)
\(\Leftrightarrow\hept{\begin{cases}2^n-1=1\\2^m-1=1\end{cases}}\Leftrightarrow m=n=1\)
Vậy m = 1 ; n = 1
7 tháng 9 2017
<br class="Apple-interchange-newline"><div id="inner-editor"></div>2m+2n=2m+n⇔2m+n−2m−2n=0
⇔2m.(2n−1)−(2n−1)=1⇔(2n−1).(2m−1)=1
⇔{
| 2n−1=1 |
| 2m−1=1 |
Vậy m = 1 ; n = 1
Đúng 4 Sai 0 Shit đã chọn câu trả lời này.
10 tháng 9 2020
\(2^m+2^n=2^{m+n}\)--->Chia 2 vế cho 2n
\(\Rightarrow2^{m-n}+1=2^m\Leftrightarrow2^m-2^{m-n}=1\)
\(\Leftrightarrow2^{m-n}\left(2^n-1\right)=1\)---> Các lũy thừa số mũ tự nhiên của 2 không thể bé hơn 1 nên pt chỉ có nghiệm khi:
\(\hept{\begin{cases}2^{m-n}=1\\2^n-1=1\end{cases}\Leftrightarrow\hept{\begin{cases}2^{m-n}=2^0\\2^n=2^1\end{cases}\Leftrightarrow}\hept{\begin{cases}m-n=0\\n=1\end{cases}\Rightarrow}m=n=1}\)
10 tháng 9 2020
\(2^m+2^n=2^{m+n}\Leftrightarrow2^m.2^n-2^m-2^n+1=1\)
\(2^m\left(2^n-1\right)-\left(2^n-1\right)=1\Leftrightarrow\left(2^m-1\right)\left(2^n-1\right)=1\)
Vì \(2^m-1\)và \(2^n-1\)đều lớn hơn 0 nên ta chỉ có một trường hợp \(\hept{\begin{cases}2^m-1=1\\2^n-1=1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\n=1\end{cases}}}\)
8 tháng 10 2016
Nếu 2m + 2n = 2m+n
thì: 2m + 2n = 2m.2n
=> 2m = 2m.2n - 2n
=> 2m = 2n.(2m-1)
=> 1 = (2n - 1).(2m-1)
còn lại bạn lập bảng tự làm nhé
10 tháng 1 2017
1) cô hướng dẫn rồi
2)ta có 1/4 =3/12=1/12+1/6
3)ta có 1/6=3/18=1/9+1/18
4) giống câu 1)
29 tháng 6 2023
program tim_nguon_nho_nhat;
const
MAX_NUMBER = 10000;
var
M, nguon_nho_nhat: Integer;
function TinhTongChuSo(num: Integer): Integer;
var
sumOfDigits: Integer;
begin
sumOfDigits := 0;
while num > 0 do
begin
sumOfDigits := sumOfDigits + (num mod 10);
num := num div 10;
end;
TinhTongChuSo := sumOfDigits;
end;
function TimNguonNhoNhat(M: Integer): Integer;
var
N, M_temp, M_digits, nguon_nho_nhat: Integer;
begin
M_temp := M;
nguon_nho_nhat := MAX_NUMBER;
for N := 1 to M_temp do
begin
M_digits := TinhTongChuSo(N) + N;
if M_digits = M_temp then
begin
if N < nguon_nho_nhat then
nguon_nho_nhat := N;
end;
end;
if nguon_nho_nhat = MAX_NUMBER then
TimNguonNhoNhat := 0
else
TimNguonNhoNhat := nguon_nho_nhat;
end;
begin
Readln(M);
nguon_nho_nhat := TimNguonNhoNhat(M);
if nguon_nho_nhat = 0 then
Writeln('0')
else
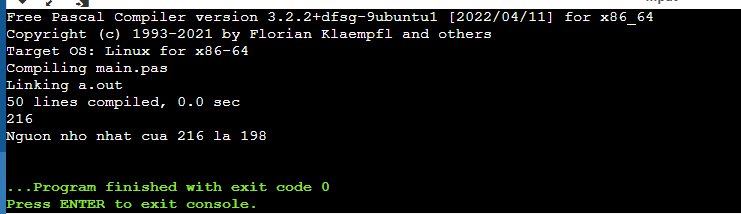
Writeln('Nguon nho nhat cua ', M, ' la ', nguon_nho_nhat);
end.
Lời giải:
Từ \(2^m+2^n=2^{m+n}=2^m.2^n\Rightarrow 2^m+2^n\vdots 2^n\)
\(\Leftrightarrow 2^m\vdots 2^n\Leftrightarrow m\geq n(1)\)
Tương tự, \(2^m+2^n=2^m.2^n\vdots 2^m\Rightarrow 2^n\vdots 2^m\Leftrightarrow n\geq m(2)\)
Từ \((1),(2)\Rightarrow m=n\). Thay vào PT ban đầu:
\(2^n+2^n=2^{2n}\Leftrightarrow 2^{n+1}=2^{2n}\Rightarrow n=1\)
Vậy PT có nghiệm \(m=n=1\)