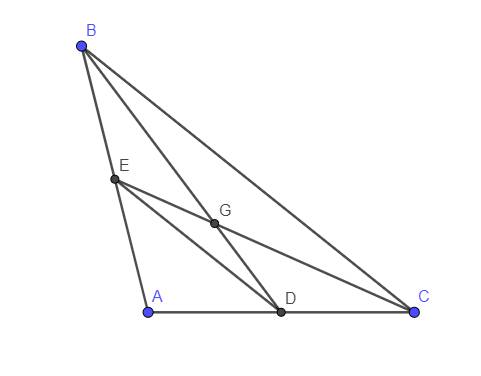
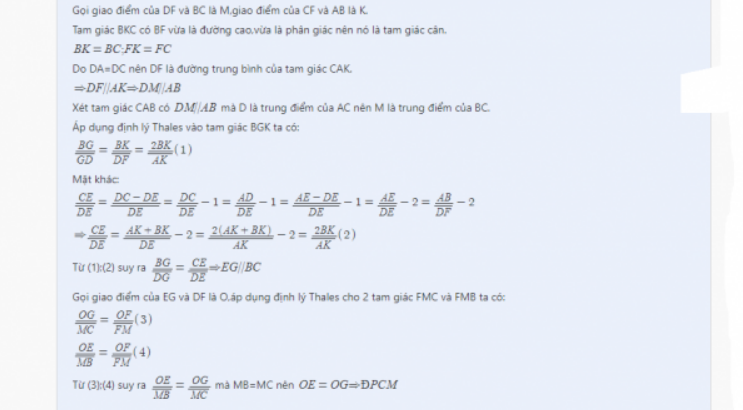
Tam giác ABC có đường trung tuyến BE, CF cắt nhau tại G, với BF + FG = CE + EG. Chứng minh tam giác ABC cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
4 tháng 3 2023
xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)
6 tháng 3 2023
a: Xét ΔABC có
AI,BE,CF vừa là trung tuyến vừa đồng quy tại G
=>G là trọng tâm của ΔABC
=>BG=2GE; CG=2GFl AG=2GI
=>BG=GN; CG=GP; AG=GM
Gọi O là giao của PM và BG
Xét tứ giác ABMN có
G là trung điểm chung của AM và BN
=>ABMN là hình bình hành
=>AN=BM
Xét tứ giác APMC có
G là trung điểm của AM và PC
=>APMC là hình bình hành
=>AP=MC
Xét tứ giác BPNC có
G là trung điểm chung của BN và PC
=>BPNC là hình bình hành
=>BP=NC và NP=BC
Xet ΔMNP và ΔABC có
MN=AB
NP=BC
MP=AC
=>ΔMNP=ΔABC
b: Xét tứ giác BPGM có
GP//BM
GP=BM
=>BPGM là hình bình hành
=>O là trung điểm của BG và PM
=>BO=OG=GE=EN
=>NG=2/3NO
Xét ΔMNP có
NO là trung tuyến
NG=2/3NO
=>G là trọng tâm của ΔMNP
