Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
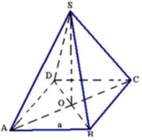
Gọi O là tâm của hình vuông ABCD.
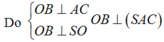
Hình chiếu vuông góc của tam giác SAB
lên (SAC) là tam giác SAO
Khi đó,
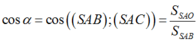
Ta có:
∆ S O A vuông tại O:
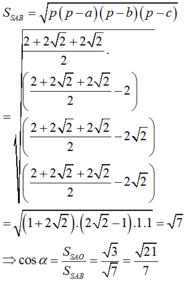
Chọn C.
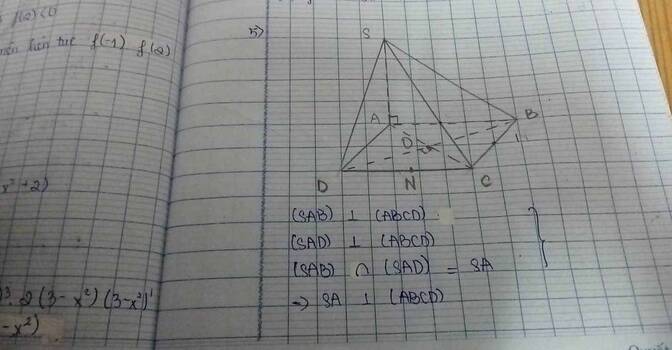
a) (SAB) và (SAD) cùng vuông góc (ABCD), (SAB) và (SAB) có giao tuyến SA => SA vuông góc (ABCD)
=> BC vuông góc SA. Mà BC vuông góc AB nên BC vuông góc (SAB).
Ta cũng có BD vuông góc AS, BD vuông góc AC vì ABCD là hình vuông
=> BD vuông góc (SAC) hay (SAC) vuông góc (SBD).
b) Gọi M là trung điểm của AB, CM cắt AD tại P, H thuộc CM sao cho AH vuông góc CM, K thuộc SH sao cho AK vuông góc SH.
Dễ thấy AN || CM => AN || (SCM) => d(AN,SC) = d(AN,SCM) = d(A,SCM) = d(A,SMP)
Ta có AH vuông góc MP, MP vuông góc AS => MP vuông góc (HAS) => (SMP) vuông góc (HAS)
Vì (SMP) và (HAS) có giao tuyến SH, AK vuông góc SH tại K nên d(A,SMP) = AK
Theo hệ thức lượng thì: \(\frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AP^2}\)
\(\Rightarrow d\left(AN,SC\right)=d\left(A,SMP\right)=AK=\frac{AS.AM.AP}{\sqrt{AS^2AM^2+AM^2AP^2+AP^2AS^2}}\)
\(=\frac{a\sqrt{2}.\frac{a}{2}.a}{\sqrt{2a^2.\frac{a^2}{4}+\frac{a^2}{4}.a^2+a^2.2a^2}}=\frac{a\sqrt{22}}{11}.\)
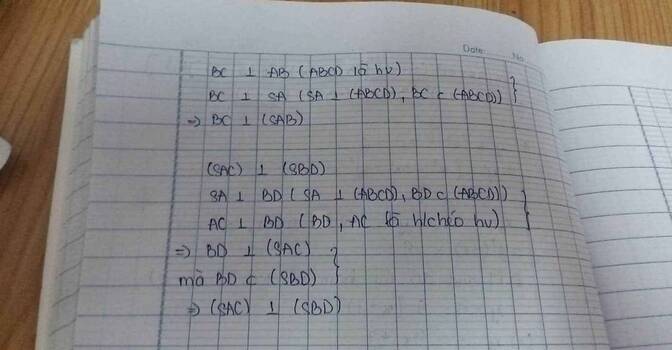
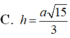
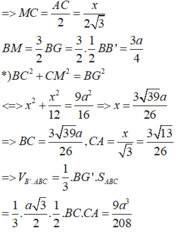
Lời giải:
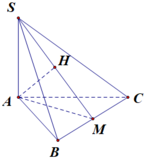
Gọi $O$ là tâm đáy thì $SO\perp (ABCD)$
Ta thấy:
$BO\perp AC, BO\perp SO\Rightarrow BO\perp (AC, SO)$
Hay $BO\perp (SAC)(*)$
Gọi $T$ là trung điểm $AB$, $OH\perp ST$.
$OT\perp AB$
$SO\perp AB$
$\Rightarrow (SOT)\perp AB$
$\Rightarrow OH\perp AB$
Mà $OH\perp ST$
$\Rightarrow OH\perp (AB, ST)$ hay $OH\perp (SAB)(**)$
Từ $(*); (**)\Rightarrow \cos a=\cos \widehat{HOB}$
Trong đó:
$BO=\frac{2\sqrt{2}}{2}=\sqrt{2}$
$SO=\sqrt{SB^2-BO^2}=\sqrt{(2\sqrt{2})^2-(\sqrt{2})^2}=\sqrt{6}$
$ST=\sqrt{SO^2+OT^2}=\sqrt{6+1}=\sqrt{7}$
$OH=\frac{SO.OT}{ST}=\frac{\sqrt{6}.1}{\sqrt{7}}=\sqrt{\frac{6}{7}}$
Vì $OH\perp (SAB)$ nên tam giác $BHO$ vuông tại $H$. Do đó:
$\cos a=\cos \widehat{HOB}=\frac{HO}{OB}=\frac{\sqrt{6}}{\sqrt{7}.\sqrt{2}}=\frac{\sqrt{3}}{\sqrt{7}}$