 mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1, What would he like to have for breakfast?
He would like to have a sandwich
2,Who would you like to go fishing with?
I would like to go fishing with my father
3,What would her children like to do in the summer?
They would like to go swimming
4,When would Mrs Tam like to go shopping?
She would like to go shopping at weekends
5,Where would Hung and Tung like to study
They would like to study in the library
1 What would he like for breakfast?
He'd like a sandwich
2 Who would you like to go fishing with?
I would like to go with my father
3 What would her children like to do in summer?
They would like to swim inpool
4 When would Mrs Tam like to go shopping?
She would like to go shopping on the weekends
5 Where would Tung and Hung like to study ?
THey would like to study in the school library

em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được

- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
Ban ơi :(( ngay chỗ dấu ngoặc nhọn đầu tiên của TH2 có công thức j k bạn?

Nếu \(y\le0\Rightarrow\left(y-4\right)^2\ge16>9\left(ktm\right)\Rightarrow y>0\)
Nếu \(x\ge0\Rightarrow\left(x+5\right)^2\ge25>9\left(ktm\right)\Rightarrow x< 0\)
Đặt \(\left\{{}\begin{matrix}-x=a>0\\y=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(a-5\right)^2+\left(b-4\right)^2\le9\\3a+b\ge14\end{matrix}\right.\)
Ta có:
\(14^2\le\left(3a+b\right)^2\le\left(3^2+1\right)\left(a^2+b^2\right)\Rightarrow a^2+b^2\ge\dfrac{196}{10}=\dfrac{98}{5}\)
\(P_{min}=\dfrac{98}{5}\) khi \(\left(a;b\right)=\left(\dfrac{21}{5};\dfrac{7}{5}\right)\) hay \(\left(x;y\right)=\left(-\dfrac{21}{5};\dfrac{7}{3}\right)\)
Lại có:
\(\left(a-5\right)^2+\left(b-4\right)^2\le9\Leftrightarrow a^2+b^2\le10a+8b-32\le\sqrt{\left(10^2+8^2\right)\left(a^2+b^2\right)}-32\)
\(\Rightarrow P\le2\sqrt{41}\sqrt{P}-32\Leftrightarrow P-2\sqrt{41}\sqrt{P}+32\le0\)
\(\Rightarrow\left(\sqrt{P}-3-\sqrt{41}\right)\left(\sqrt{P}-3+\sqrt{41}\right)\le0\) (1)
Do \(P\ge\dfrac{98}{5}\Rightarrow\sqrt{P}-3+\sqrt{41}>0\)
Nên (1) tương đương: \(\sqrt{P}-3-\sqrt{41}\le0\Rightarrow P\le50+6\sqrt{41}\)
\(P_{max}=50+6\sqrt{41}\) khi \(\left(a;b\right)=\left(5+\dfrac{15}{\sqrt{41}};4+\dfrac{12}{\sqrt{41}}\right)\)

1
Có: \(tgB=\dfrac{CA}{CB}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
\(cotgB=\dfrac{CB}{CA}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)
Vì A, B phụ nhau nên:
\(cotgA=tgB=\dfrac{3}{4}\\ tgA=cotgB=\dfrac{4}{3}\)
Áp dụng pytago vào tam giác ABC vuông tại C, có:
\(AB^2=BC^2+AC^2=1,2^2+0,9^2=1,5^2\Rightarrow AB=1,5\left(vì.AB>0\right)\)
Do đó: \(sinB=\dfrac{CA}{AB}=\dfrac{0,9}{1,5}=\dfrac{3}{5};cosB=\dfrac{CB}{BA}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)
Vì A, B phụ nhau nên:
\(sinA=cosB=\dfrac{4}{5};cosA=sinB=\dfrac{3}{5}\)
3:
a: Xét ΔBAC có AB^2=CA^2+CB^2
nên ΔABC vuông tại C
b: sin A=cos B=BC/AC=căn 15/5
cos A=sin A=CA/BC=căn 2/5=1/5*căn 10
tan A=cot B=căn 15/căn 10=căn 3/2
cot A=tan B=căn 2/3


\(B=\left(x-8x-3\right)\)
\(B=\left(x^2-2x4-16\right)+13\)
\(-B=\left(x^2+2x4+16\right)-13\)
\(-B=\left(x+4\right)^2-13\ge-13\)
\(B=-\left(x+4\right)^2+13\le13\)
Dấu "=" xảy ra khi và chỉ khi \(-\left(x+4\right)^2=0\)
\(\Leftrightarrow\left(x+4^2\right)=0\)
\(\Leftrightarrow x+4=0\)
\(\Leftrightarrow x=-4\)
Vậy GTLN của B là 13 khi và chỉ khi x=-4




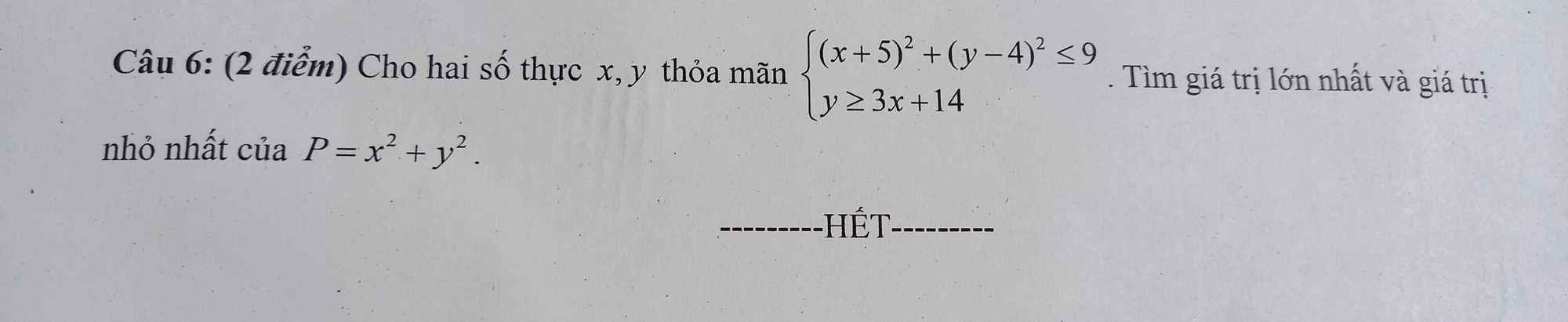


 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Xét pt hoành độ gđ của đường thẳng và parabol có:
\(\left(m-1\right)x^2+3mx+2m=2x-1\)
\(\Leftrightarrow\left(m-1\right)x^2+x\left(3m-2\right)+2m+1=0\) (1)
Để đt và parabol cắt tại hai điểm pb có hoành độ âm
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S< 0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m+8>0\\\dfrac{2-3m}{m-1}< 0\\\dfrac{2m+1}{m-1}>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;4-2\sqrt{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\\m\in\left(-\infty;\dfrac{2}{3}\right)\cup\left(1;+\infty\right)\\m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(1;+\infty\right)\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\)
Vậy...