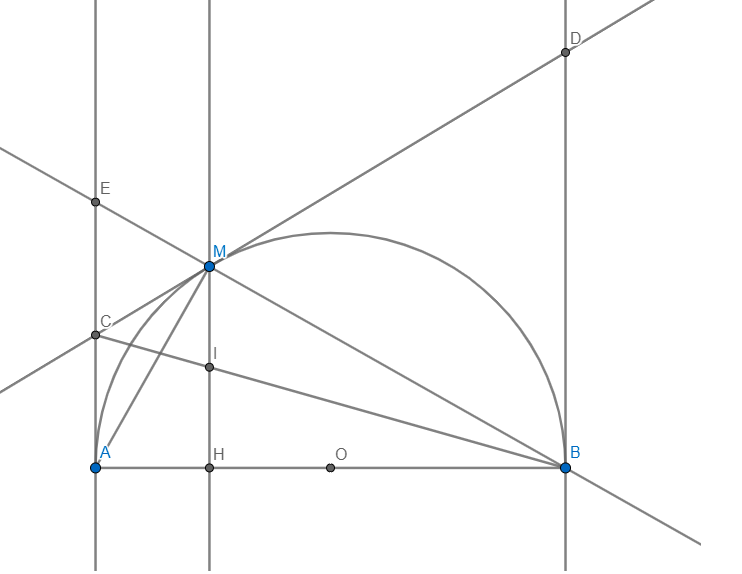
Cho nửa đường tròn tâm (O) đường kính AB=2R . Trên nửa đường tròn lấy điểm M sao cho . Vẽ các tiếp tuyếnAx, By ( cùng thuộc một nửa mặt phẳng bờ có chứa điểm ). Tiếp tuyến tại M của đường tròn cắt lần lượt tại Ax.By lần lượt tại C và D .
1) Chứng minh tứ giác OBMD là nội tiếp
2) BC cắt đường tròn tại F ( F khác B). Đường thẳng qua O vuông góc với BC cắt By tại E . Chứng minh: EF là tiếp tuyến của đường tròn .
3) Gọi K là giao điểm của OE và BC . Chứng minh: KO.KE= KF.KBvà đường trung trực của đoạn thẳng MK đi qua điểm .D

a. xét tứ giác OBMD có
∠DBO=90 ( tiếp tuyến By)
∠OMD=90 (tiếp tuyến tại M)
⇒∠DBO+∠OMD=90+90=180
⇒tứ giác OBMD nội tiếp
b.ΔOBF cân tại O do OB=OF=R
⇒∠B1=∠F1 (1)
có ∠E1=∠B1 (cùng phụ ∠EOB) (2)
từ (1);(2) ⇒∠F1=∠E1 (cùng nhìn OB)
⇒OFEB nội tiếp
⇒∠OFE=∠OBE=90
⇒EF⊥OF
⇒EF là tiếp tuyến của (O)
c. xét ΔKFO và ΔKEB có
∠FKO=∠EKB=90
∠E1=∠F1
⇒ΔKFO ∼ ΔKEB (g.g)
⇒\(\dfrac{KO}{KB}=\dfrac{KF}{KE}\)⇒KO.KE=KF.KB