Cho ba điểm A( -6;3) ;B( 0; -1) và C( 3;2). Tìm điểm M trên đường thẳng d : 2x- y + 3= 0 mà M A → + M B → + M C → nhỏ nhất là:
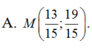
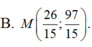
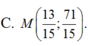
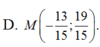
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi A B → , A C → cùng phương
![]()

Chọn B.
Ta có M nằm trên trục Oy nên tọa độ điểm M có dạng M(0; y)
Ba điểm A; B; M thẳng hàng khi ![]() cùng phương với
cùng phương với ![]()
Ta có ![]() . Do đó,
. Do đó, ![]() cùng phương với
cùng phương với
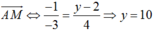
Vậy M(0; 10) .

a) Dựa vào độ dài đã cho của các đoạn thẳng ta nhận thấy rằng MN + NP ≠ MP nên điểm N không nằm giữa hai điểm M và P.
Tương tự, điểm M không nằm giữa hai điểm N và P, điểm P không nằm giữa hai điểm M và N.
Từ đó suy ra ĐPCM.
b) Theo ý a), không có điểm nào nằm giữa hai điểm còn lại nên ba điểm M, N, P không thẳng hàng.
Đáp án D
Do M thuộc d nên M( x; 2x+ 3)
Suy ra:
Do đó:
nhỏ nhất khi và chỉ khi: f(x) = 45x2+ 78x + 34 nhỏ nhất